|
Пусть 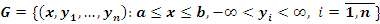 - множество в - множество в 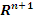 и и 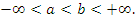
Определение. Взаимно – однозначное отображение 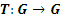 называют преобразованием. называют преобразованием.
Преобразование Т переводит каждую точку 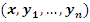 в некоторую точку в некоторую точку 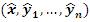 и может быть выражено функционально в виде и может быть выражено функционально в виде
| |
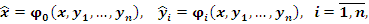
|
(1) |
|
где 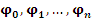 - некоторые функции. - некоторые функции.
Рассмотрим семейство преобразований 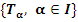 из G в G, где I – некоторое множество индексов в из G в G, где I – некоторое множество индексов в 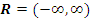 или или 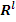 , причем точка O является предельной точкой для I, то есть в любой окрестности O существуют точки из I. Функционально это семейство преобразований задается в виде , причем точка O является предельной точкой для I, то есть в любой окрестности O существуют точки из I. Функционально это семейство преобразований задается в виде
| |
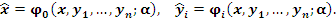
|
(2) |
|
Предположим, что эти функции дифференцируемые и при 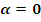 преобразование преобразование 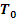 тождественно, то есть тождественно, то есть 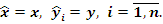
Возьмем некоторую непрерывно дифференцируемую функцию 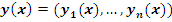 на (a, b), и выделим отрезок кривой на (a, b), и выделим отрезок кривой 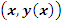 , заключенный между точками , заключенный между точками 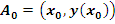 и и 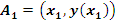 , где , где 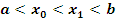 . Обозначим его . Обозначим его 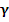 , то есть , то есть
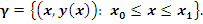
Под действием 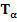 отрезок кривой отрезок кривой 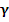 преобразуется в кривую преобразуется в кривую 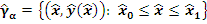 . .
Рассмотрим теперь функционал от 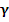
| |

|
(3) |
|
Для преобразованной кривой 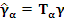 этот функционал принимает некоторое значение этот функционал принимает некоторое значение
| |
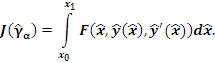
|
(4) |
|
Определение. Функционал 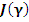 называется инвариантным относительно семейства преобразований называется инвариантным относительно семейства преобразований 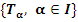 , задаваемого равенствами (*), если для любого , задаваемого равенствами (*), если для любого 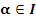
| |
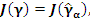
|
(5) |
|
где 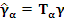 . .
Пример инвариантного преобразования.
Пусть 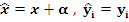 , то есть точка , то есть точка 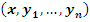 переводится преобразованием переводится преобразованием 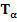 в точку в точку 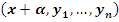 . .
Под действием 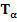 кривая кривая 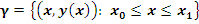 преобразуется в кривую преобразуется в кривую 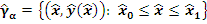 . При этом точка . При этом точка 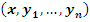 переходит в точку переходит в точку
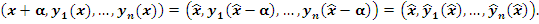
Отсюда находим
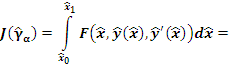
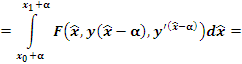
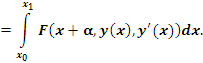
В результате мы приходим к следующему заключению.
Предложение 1. Пусть семейство преобразований 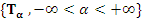 задается равенством (2) и функция задается равенством (2) и функция 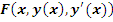 не зависит явно от х. не зависит явно от х.
Тогда функционал 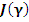 , определяемый равенством (3), инвариантен относительно семейства преобразований , определяемый равенством (3), инвариантен относительно семейства преобразований 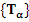 . .
|
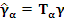 .
.