|
Рассмотрим задачу оптимизации функционалов вида
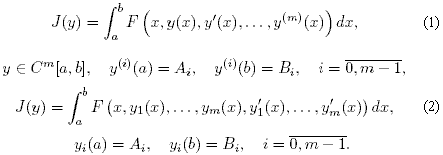
Если функция F в (2) имеет непрерывные производные
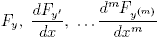
и существует функция y(·), доставляющая экстремум этому функционалу, то она удовлетворяет уравнению Эйлера
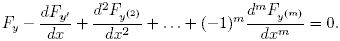
Пример 1. Найти минимум функционала
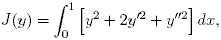
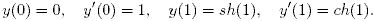
Имеем Fy = 2y, Fy' = 4y',
Fy'' = 2y''. Решаем уравнение Эйлера
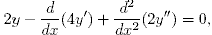
или
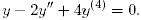
Это линейное уравнение четвертого порядка с постоянными коэффициентами имеет общее решение
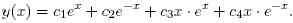
Определяя постоянные c1,..., c4 из граничных условий, получаем
y0(x) = sh (x).
Нетрудно проверить, что эта функция доставляет глобальный минимум функционалу.
Пример 2. Найти минимум функционала
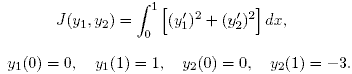
Составляем систему уравнений Эйлера
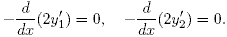
Решая эту систему с учетом граничных условий, получаем
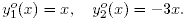
Непосредственной подстановкой в приращение функционала
J (y1, y2) = J (y1 + h1, y2 + h2) - J (y1, y2)
убеждаемся, что для функций y10(x), y20(x)
функционал J (y1, y2) имеет глобальный минимум.
|