Уравнение Эйлера: пример

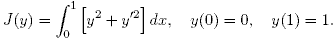
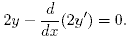
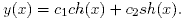
Найдем функцию  y( · ), доставляющую минимум функционалу        Имеем:  F (x1, x2, x3) = x22 + x32. Поскольку частные производные функции  F  по переменным  x2  и  x3  равны  2x2  и  2x3  сответственно, то уравнение Эйлера имеет вид        Отсюда   y''  –  y = 0.        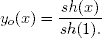Решая это уравнение, получаем        Учитывая граничные условия, получаем  c1 = 0,  c2 = 1 / sh(1), то есть экстремаль определяется формулой        Покажем, что функция  y0(x)  доставляет глобальный минимум функционала  J (y).        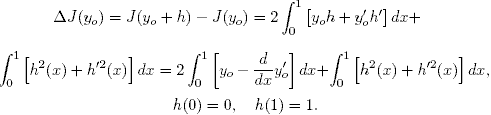Рассмотрим приращение        Так как  y0(x)  удовлетворяет уравнению Эйлера, то  ∆J ( y0(x) ) > 0  при  h ≠ 0.