|
|
| Основная лемма вариационного исчисления |
|
|
|
|
Лемма. Если функция f (x), a ≤ x ≤ b, непрерывна и для любой
непрерывной функции h (x), a ≤ x ≤ b,
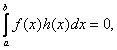
Доказательство. Предположим противное: пусть f (x) ≠ 0 и существует точка
х0, a < х0 < b, такая, что
f (x) = m > 0.
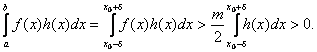
|
|
|