-
Экстремумы функций
Напомним основные понятия и результаты, относящиеся к проблеме нахождении экстремума дифференцируемой функции
u = u(P) одной или нескольких переменных. (Здесь P –
произвольная точка в пространстве соответствующей размерности.)
Точка P0 является точкой минимума функции
u(P), если
| |
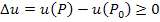
|
(1) |
|
для всех точек P, принадлежащих достаточно малой окрестности точки P0 .
Точка P0 является точкой максимума функции
u(P), если
| |
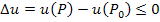
|
(2) |
|
для всех точек P, принадлежащих достаточно малой окрестности точки P0 .
Точка P0 является точкой экстремума функции
u(P), если приращение
Δu сохраняет свой знак для всех точек P, принадлежащих достаточно малой окрестности точки
P0 .
Необходимым условием наличия у функции u экстремума в точке P0 является
обращение в нуль в этой точке ее дифференциала:
| |
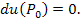
|
(3) |
|
Справедливость этого утверждения легко доказать от противного. Действительно, в первом приближении приращение функции
u в точке экстремума можно представить в виде
Δu = du. Предположим, что дифференциал функции
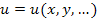 в точке
P0 отличен от нуля: в точке
P0 отличен от нуля:
| |
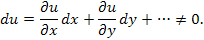
|
(4) |
|
Тогда линейность формы дифференциала функции относительно приращений dx, dy, ... означает, что при
изменении направления смещения из точки P0 на противоположное изменяют свои знаки дифференциал и
приращение функции u и, следовательно, точка P0
не является точкой экстремума.
Заметим, что условие (3) влечет за собой равенство нулю в точке экстремума всех частных производных функции u.
| |
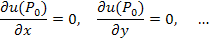
|
(5) |
|
-
Оптимизация функционалов
Вариация функционала 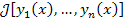 обращается в нуль
на кривых, на которых достигается экстремум функционала. Такие кривые называются экстремалями функционала. обращается в нуль
на кривых, на которых достигается экстремум функционала. Такие кривые называются экстремалями функционала.
Необходимое условие существования экстремали функционала 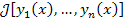 описывается
уравнением описывается
уравнением
| |
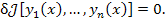
|
(6) |
|
Интуитивный подход, основанный на сопоставлении понятий дифференциального и вариационного исчислений, позволяет сформировать на
определенном уровне восприятия более или менее стройные представления о ключевых концепциях вариационного исчисления.
Однако следует с большой долей осторожности относиться к использованию аналогий, пытяясь распространить
привычные утверждения в сферу действий с объектами другой природы. Некоторые данные в параллель понятия вариационного исчисления
нуждаются в уточнениях и дополнениях.
Во-первых, требуется уточнить критерии выбора допустимого класса функций, в котором выбирается оптимальная функция в смысле
минимизации функционала 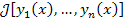 . Выбор допустимого класса функций требует конкретизации
типа задач, решение которых связано с оптимизацией функционала. Например, для нахождения траектории перехода частицы из одной точки в
другую в качестве допустимого класса функций должны выступать функции с закрепленными концами (в начальной и конечной точках
траектории). При изучении другого круга задач границы могут рассматриваться как подвижные и так далее. . Выбор допустимого класса функций требует конкретизации
типа задач, решение которых связано с оптимизацией функционала. Например, для нахождения траектории перехода частицы из одной точки в
другую в качестве допустимого класса функций должны выступать функции с закрепленными концами (в начальной и конечной точках
траектории). При изучении другого круга задач границы могут рассматриваться как подвижные и так далее.
Во-вторых, следует сформулировать уравнения, выражающие неободимое условие существования экстремума функционала
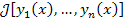 в терминах функциональных производных
функционала по функциям yi (x) (i = 1, ..., n),
которые являлись бы аналогом уравнений (5) из дифференциального исчисления. в терминах функциональных производных
функционала по функциям yi (x) (i = 1, ..., n),
которые являлись бы аналогом уравнений (5) из дифференциального исчисления.
В вариационном исчислении такие уравнения называются уравнениями Эйлера, которые отличается по сути и по форме от
аналогичных уравнений из дифференциального исчисления. Для функционалов, используемых в физических приложениях, уравнение Эйлера в
большинстве случаях представляет собой обыкновенное дифференциальное уравнение второго порядка
(или систему дифференциальных уравнений второго порядка).
|