| Функции |
Функционалы |
Обозначение функции одной переменной:
y = f (x).
Суть понятия: Правило, устанавливающее соответствие между элементами двух числовых множеств.
Аргумент функции y = f (x): Переменная x, множество допустимых значений которой образует область определения функции.
Обозначение функции нескольких переменных:
y = f (P), где
P (x1, x2, ...,
xn ) – точка некоторой области
D n-мерного пространства.
Суть понятия: Правило, устанавливающее соответствие между точками области D и
значениями функции y.
Аргумент функции y = f (P):
Вектор (x1, ..., xn), составленный из вещественных переменных
x1, x2, ...,
xn . |
Обозначение функционала одной переменной: 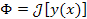 . .
Суть понятия: Правило, устанавливающее соответствие между элементами y (x)
некоторого функционального множества и элементами Φ числового множества. Иначе говоря, каждой функции
y (x) из некоторого класса функций ставится в соответствие число Φ.
Аргумент функционала 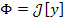 : Функциия
y (x) вещественной переменной x или функция
y = y (x1 , ... , xn )
нескольких переменных
x1, ..., xn . : Функциия
y (x) вещественной переменной x или функция
y = y (x1 , ... , xn )
нескольких переменных
x1, ..., xn .
Область определения функционала 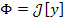 : Совокупность функций
y (P), удовлетворяющих заданным условиям. : Совокупность функций
y (P), удовлетворяющих заданным условиям.
Аргументом функционала 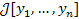 является упорядоченный
набор функций y1 , ... , yn
вещественной переменной х. является упорядоченный
набор функций y1 , ... , yn
вещественной переменной х. |
Примеры:
-
Выражение
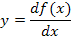 представляет собой некоторую функцию (производную от
функции f (x)), тогда как выражение представляет собой некоторую функцию (производную от
функции f (x)), тогда как выражение
 может рассматриваться в качестве функционала. может рассматриваться в качестве функционала.
-
Неопределенный интеграл
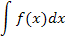 представляет собой некоторую функцию, тогда как
определенный интеграл представляет собой некоторую функцию, тогда как
определенный интеграл 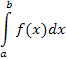 является функционалом. является функционалом.
|
| Функция y = f (P) является непрерывной, если бесконечно малое
изменение аргумента влечет за собой бесконечно малое изменение значения функции y. |
Функционал 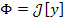 называется непрерывным, если малому изменению
функции y (P) соответствует малое изменение значения функционала Φ. называется непрерывным, если малому изменению
функции y (P) соответствует малое изменение значения функционала Φ. |
Под дифференциалом независимой переменной некоторой функции
y = f (P) понимается произвольное приращение этой переменной (в пределах области
определения функции f ).
Приращение функции f прелставляет собой ее изменение Δf ,
обусловленное приращением аргумента функции.
Приращение Δf функции y = f (x) можно представить в
виде:
Δf = f = f (x + Δx) – f (x) =
= A dx + 0(dx),
где A dx – главная линейная часть приращения функции;
0(dx) – бесконечно малая величина более высокого порядка по сравнению с dx.
Дифференциал функции y = f (x) определяется как главная
линейная часть ее приращения относительно дифференциала аргумента: df = A dx.
|
Вариация функции y (x) представляет собой произвольную функцию η (x), добавление которой к функции y (x) не изменяет ее принадлежности к заданному классу функций:
Приращение функционала 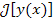 представляет собой разность представляет собой разность
Вариация функционала представляет собой главную линейную часть приращения функционала относительно вариации его аргумента:
|
|