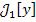 уравнением
уравнением
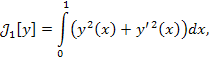
Если y = sin x, то
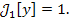
Если y = x2, то
| Функционалы |
Пример 1. Определим функционал 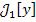 уравнением уравнением
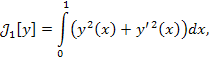
Если y = sin x, то 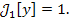
Если y = x2, то 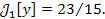
|
Пример 2. Одно из основных свойств дельта-функции Дирака выражается формулой
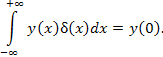
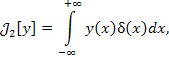 сопоставляющего каждой функции y (x) ее значение при x = 0:
сопоставляющего каждой функции y (x) ее значение при x = 0:
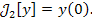
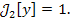
Любой интеграл, содержащий под своим знаком δ-функцию, может рассматриваться в качестве функционала подобного вида. |
Пример 3. Рассмотрим представление периодической функции f (x) с периодом
2L в виде ряда Фурье:
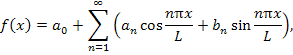
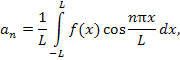
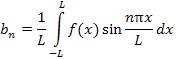
и фактически представляют собой функционалы An [f (x)] и Bn [f (x)], заданные в классе периодических функций, удовлетворяющих условиям Дирихле. |
Пример 4. Площадь криволинейной трапеции, ограниченной сверху линией
y = f (x), с боков – вертикальными отрезками
x = a и
x = b, снизу – осью 0x, описывается формулой
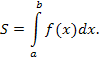
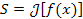 . .
|
Пример 5. Длина дуги плоской кривой y = f (x), заключенной
между точками x = a и x = b, описывается формулой
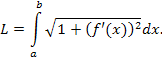
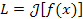 . .
|