|
Вариационное исчисление представляет собой раздел математики, в котором обобщается теория экстремума функций одной или нескольких
переменных на случай функционалов соответствующего числа переменных.
Процитируем Эльсгольца Л.Э., автора получившего широкую известность учебника «Дифференциальные уравнения и вариационное исчисление»:
"Многие законы механики и физики сводятся к утверждению, что некоторый функционал в рассматриваемом процессе должен достигать
минимума или максимума. В такой формулировке эти законы носят название вариационных принципов механики или физики. К числу таких
вариационных принципов или простейших следствий из них принадлежат: принцип наименьшего действия, закон сохранения энергии,
закон сохранения импульса, закон сохранения количества движения, закон сохранения момента количества движения, различные
вариационные принципы классической и релятивистской теории поля, принцип Ферма в оптике, принцип Кастилиано в теории упругости и т.д."
В основе вариационного исчисления лежит понятие функционала, то есть функция
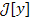 , аргумент которой сам является функцией. , аргумент которой сам является функцией.
Одной из основных задач вариационного исчисления является нахождение экстремумов функционалов. Подобно тому, как в задаче о нахождении наибольшего и наименьшего значений функции необходимо указать область изменения её
аргументов, для соответствующей функционала следует задать класс допустимых функциональных аргументов. Например, можно говорить о классе функций,
непрерывных вместе с первыми производными в некоторой области и удовлетворяющих заданным условиям на границе области.
Однако не следует проводить абсолютные параллели между исследованиями функций и функционалов на экстремумы. Например, задача об
экстремуме непрерывной функции всегда имеет решение, поскольку непрерывная функция достигает своих наибольшего и наименьшего значений
внутри заданной области или на её границе, тогда как существование экстремума функционала для данного класса функциональных аргументов
не гарантировано и может быть установлено только в результате исследования.
Обсудим простейшие понятия вариационного исчисления, основываясь на соответствующих представлениях, лежащих в основе
классической теории функций.
-
Функции
Задание функции y = f (x) вещественной переменной x означает, что
каждому значению x из некоторого числового множества ставится в соответствие
число y.
Пример 1. Если f (x) = x2, то y(2) = 4
и y(3) = 9.
Аналогично определяется числовая функция нескольких переменных.
Например, функция
f (x, y) двух переменных x и y
определяется заданием правила сопоставления каждой упорядоченной паре чисел (х,у) из некоторого числового
множества Е числа z = f (x,y).
Пример 2. Пусть f (x, y) = x2 +
y2. Тогда f (3,4) = 25.
Аргументом функции y = f (x) является вещественная переменная x,
аргументом функции
y = f (x1, ..., xn) является вектор
(x1, ..., xn), составленный из вещественных переменных
x1, ..., xn.
Областью определения функции y = f (x) является множество
Е допустимых значений переменной x. Например, областью определения функции
y = ln x является множество всех положительных чисел.
Функция y = f (x) непрерывна, если малому изменению переменной
x отвечает малое изменение функции f (x).
Функция y = f (x1 , ... , xn) непрерывна,
если при достаточно малых изменениях переменных x1, ... , xn мало и
изменение функции f.
-
Функционалы
Задание функционала 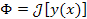 означает, что каждой функции
y (x) из некоторого класса функций, определенных на числовом множестве,
ставится в соответствие число Φ. означает, что каждой функции
y (x) из некоторого класса функций, определенных на числовом множестве,
ставится в соответствие число Φ.
Пример 3. Пусть 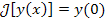 . Тогда . Тогда
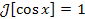 и и 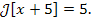
Пример 4. Областью определения функционала может являться класс дифференцируемых функций с закрепленными границами
(принимающих одинаковые значения на каждом из концов интервала [a, b]). В частности, функции вида
x, x2, x3, ...
принимают одинаковые значения на каждом из концов интервала [0, 1] и принадлежат к классу функций с закрепленными границами.
Аргументом функционала 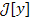 является функция y = y (x)
вещественной переменной x или функция
y = y (x1 , ... , xn ) вещественных переменных
x1, ..., xn .
Аргументом функционала является функция y = y (x)
вещественной переменной x или функция
y = y (x1 , ... , xn ) вещественных переменных
x1, ..., xn .
Аргументом функционала 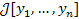 является упорядоченный
набор функций y1 , ... , yn вещественной переменной х. является упорядоченный
набор функций y1 , ... , yn вещественной переменной х.
Область определения функционала представляет собой некоторый класс функций (или некоторый класс наборов функций).
Поэтому для задания области определения функционала нужно не только указать числовое множество, на котором определены такие функции,
но и сформулировать дополнительные требования, предъявляемые к этим функциям: a) непрерывность, b) дифференцируемость,
c) равенство значений функций на концах некоторого интервала и так далее.
Например, задавая функционал 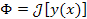 , можно потребовать, чтобы функции
y = y (x) были определены на отрезке [0,1], непрерывны, имели непрерывные
производные y'(x) и удовлетворяли условию y(0) = y(1). , можно потребовать, чтобы функции
y = y (x) были определены на отрезке [0,1], непрерывны, имели непрерывные
производные y'(x) и удовлетворяли условию y(0) = y(1).
(Этому классу принадлежат, в частности, функции x, x2, x3, ...)
Функционал 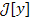 называется непрерывным, если малому изменению y (x)
соответствует малое изменение называется непрерывным, если малому изменению y (x)
соответствует малое изменение 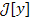 . .
|
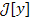 , аргумент которой сам является функцией.
, аргумент которой сам является функцией.