Показать, что векторное поле
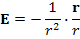
Решение.
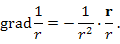
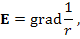
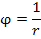 – потенциал поля E.
– потенциал поля E.
| Потенциальное поле |
|
Пример 1. Пусть r – радиус-вектор точки M (x, y, z).
Показать, что векторное поле 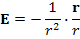
Решение. 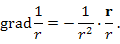
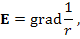
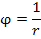 – потенциал поля E. – потенциал поля E.
|
Пример 2. Пусть r – радиус-вектор точки M (x, y, z) и 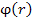 – произвольная дифференцируемая функция. – произвольная дифференцируемая функция.
Показать, что векторное поле вида 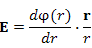
Решение. 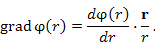
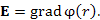
Таким образом, любое скалярное поле вида 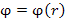 является потенциалом некоторого векторного поля. является потенциалом некоторого векторного поля.
|
Пример 3. Показать, что векторное поле
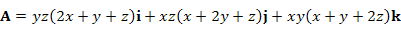
Решение. 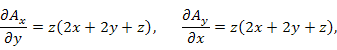
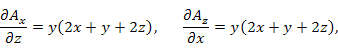
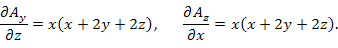
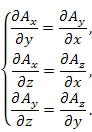
|
Пример 4. Показать, что векторное поле
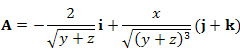
Решение. 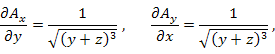
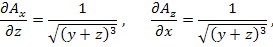
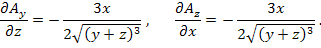
|