Представим функции f (x) и g (x) в виде их разложений в обобщенные ряды Фурье по полному набору функций  , ортогональных на промежутке
(a, b):
| |
|
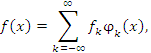
(1) |
|
| |
|
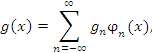
(2) |
|
где fn и gn – соответствующие коэффициенты Фурье:
| |
|
(3) |
|
| |
|
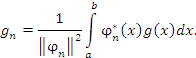
(4) |
|
Тогда скалярное произведение функций f (x) и g (x) на
промежутке (a, b) можно представить в виде
| |
|
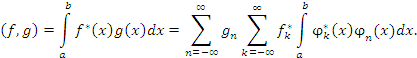
(5) |
|
Учитывая условие ортогональности
| |
|
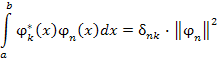
(6) |
|
и свойство
| |
 
|
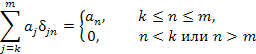
(7) |
|
дельта-символа Кронекера, получаем следующее равенство:
| |
|
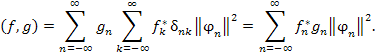
(8) |
|
Если функции нормированы на единицу на промежутке
(a, b), то
| |
|
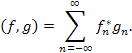
(9) |
|
В частном случае, когда g (x) = f (x), из формулы (9) вытекает
равенство Парсеваля:
| |
|
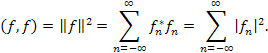
(10) |
|
|
