|
|
| Ряд Фурье и коэффициенты Фурье |
|
|
|
|
Пусть некоторая функция f (x) представлена в виде разложения по полному набору функций 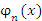 , ортогональных на промежутке (a, b): , ортогональных на промежутке (a, b):
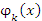 и f(x) на этом промежутке: и f(x) на этом промежутке:
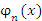 нормированы на единицу, то нормированы на единицу, то
|
|
|