|
Функции f (x) и g (x) называются ортогональными
на промежутке (a, b), если их скалярное произведение равно нулю:
| |
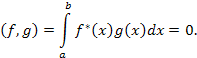
|
(1) |
|
Если функции 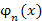 некоторого полного набора являются ортогональными на промежутке (a, b), то скалярное произведение некоторого полного набора являются ортогональными на промежутке (a, b), то скалярное произведение  удовлетворяет условию ортогональности удовлетворяет условию ортогональности
| |
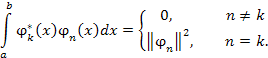
|
(2) |
|
Это условие можно также представить в виде
| |

|
(3) |
|
где 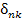 – дельта-символ Кронекера, определяемый формулой – дельта-символ Кронекера, определяемый формулой
| |
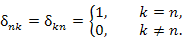
|
(4) |
|
Заметим, что дельта-символ Кронекера “снимает” суммирование в выражениях вида 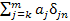 : :
| |
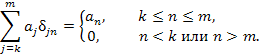
|
(5) |
|
Функции 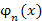 , нормированные на единицу и ортогональные на промежутке (a, b), называются ортонормированными. Условие ортонормированности функций , нормированные на единицу и ортогональные на промежутке (a, b), называются ортонормированными. Условие ортонормированности функций 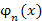 имеет вид имеет вид
| |
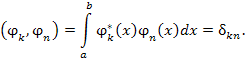
|
(6) |
|
Для сравнения приведем условие ортогональности единичных векторов 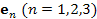 трехмерного векторного пространства: трехмерного векторного пространства:
| |
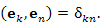
|
(7) |
|
Сходство формулы
| |
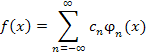
|
(8) |
|
разложения функции f (x) по полному набору фунуций  с формулой с формулой
| |
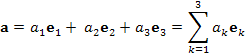
|
(9) |
|
разложения вектора a по базису векторного пространства – равно как и сходство условий ортонормированности (6) и (7) – не является чисто внешним, а выражает собой тот факт, что обычные вещественные функции могут рассматриваться в качестве векторов бесконечномерного векторного пространства, базис которого составляют функции полного набора (в общем случае – комплексные).
Если элементами такого базиса являются ортонормированные функции, то говорят, что их совокупность образует гильбертово пространство.
|
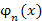 некоторого полного набора являются ортогональными на промежутке (a, b), то скалярное произведение
некоторого полного набора являются ортогональными на промежутке (a, b), то скалярное произведение  удовлетворяет условию ортогональности
удовлетворяет условию ортогональности
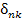 – дельта-символ Кронекера, определяемый формулой
– дельта-символ Кронекера, определяемый формулой
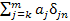 :
:
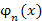 , нормированные на единицу и ортогональные на промежутке (a, b), называются ортонормированными. Условие ортонормированности функций
, нормированные на единицу и ортогональные на промежутке (a, b), называются ортонормированными. Условие ортонормированности функций 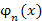 имеет вид
имеет вид
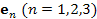 трехмерного векторного пространства:
трехмерного векторного пространства:
 с формулой
с формулой