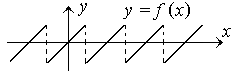Можно показать, что функции 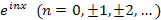 образуют полный ортогональный набор на
промежутке (0,2π) в классе периодических функций с периодом T = 2π. образуют полный ортогональный набор на
промежутке (0,2π) в классе периодических функций с периодом T = 2π.
Для доказательства периодичности семейства функций 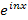 с периодом 2π
достаточно воспользоваться формулой Эйлера: с периодом 2π
достаточно воспользоваться формулой Эйлера:
| |
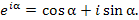 
|
(1) |
|
Тогда
где 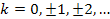
Линейная комбинация периодических функций также представляет собой периодическую функцию.
Ортогональность функций 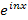 проверяется непосредственно: проверяется непосредственно:
| |
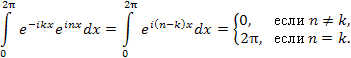 
|
(3) |
|
Одновременно установлено, что норма функций 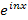 на промежутке (0,2π) равна на промежутке (0,2π) равна
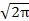 . .
Таким образом, периодическая функция f (x) с периодом T = 2π допускает
представление в виде ряда Фурье
| |
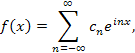 
|
(4) |
|
коэффициенты которого определяются формулой
| |
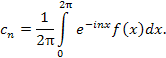 
|
(5) |
|
Разумеется, что для существования интеграла (5) необходимо выполнение определенных условий, которые принято называть условиями
Дирихле, в соответствии с которыми предполагается, что
-
на любом конечном промежутке функция f (x) может иметь разве что конечное число точек разрыва первого рода;
-
на любом конечном промежутке функция f (x) может иметь разве что конечное число точек экстремума.
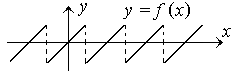 Рис. 1
Рис. 1. Пример функции, удовлетворяющей условиям Дирихле и допускающей представление в виде ряда Фурье.
Заметим, что разрывные функции не допускают представлений в виде степенных рядов.
|
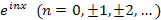 образуют полный ортогональный набор на
промежутке (0,2π) в классе периодических функций с периодом T = 2π.
образуют полный ортогональный набор на
промежутке (0,2π) в классе периодических функций с периодом T = 2π.
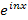 с периодом 2π
достаточно воспользоваться формулой Эйлера:
с периодом 2π
достаточно воспользоваться формулой Эйлера:
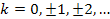
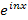 проверяется непосредственно:
проверяется непосредственно:
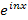 на промежутке (0,2π) равна
на промежутке (0,2π) равна
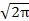 .
.