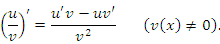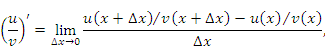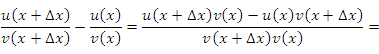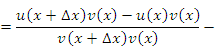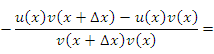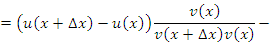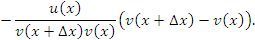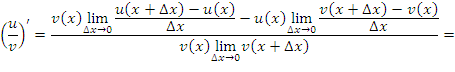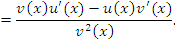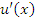Правила дифференцирования функций
Правило 3. Если существуют производные    и 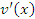  , то выполняется следующее правило дифференцирования произведения функций:
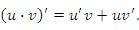
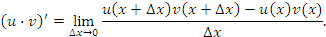
Доказательство. По определению производной


Преобразуем выражение в числителе, вычитая и прибавляя произведение 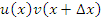 ; затем сгруппируем слагаемые:





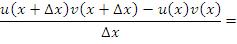
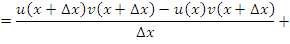
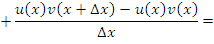
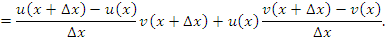
Выполняя предельный переход и учитывая, что


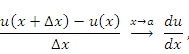
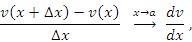
получим требуемое утверждение.

***
Правило 4. Если существуют производные    и   , то выполняется следующее правило дифференцирования частного от деления функций:
Доказательство этого правила по своей сути не отличается от предыдущего:







Учитывая свойства пределов функций, получим требуемый результат:


Закрыть окно