.
Решение. Первообразная подынтегральной функции является неограниченной функцией в окрестности особой точки x = 0 :
| Эталонные p-интегралы для неограниченных функций |
|
Пример 1. Вычислить несобственный интеграл .
Решение. Первообразная подынтегральной функции является неограниченной функцией в окрестности особой точки x = 0 :
|
Пример 2. Вычислить несобственный интеграл  .
Решение. Первообразная функция является непрерывной функцией в особой точке x = 0 :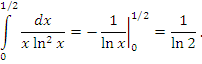 
|
Пример 3. Исследовать на сходимость несобственный интеграл  .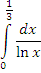
Решение. Поскольку в окрестности особой точки x = 0 выполняется неравенство 
 расходится, то расходится и исследуемый интеграл.
|
Пример 4. Вычислить несобственный интеграл  .
Решение. Интеграл расходится, поскольку первообразная функция неограничена в окрестности особой точки x = 1: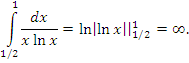 
|
Пример 5. Вычислить несобственный интеграл  .
Решение. Первообразная функция обращается в бесконечность в особой точке x = 1: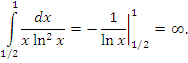 
|
Пример 6. Исследовать на сходимость несобственный интеграл  .
Решение. В окрестности особой точки x = 1 подынтегральная функция является бесконечно большой порядка 1/2 по сравнению с 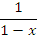 . Следовательно, интеграл сходится.
|
Пример 7. Исследовать на сходимость несобственный интеграл  .
Решение. Особой точкой является x = y, в окрестности которой разность косинусов имеет тот же порядок малости, что и разность их аргументов:  .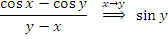
 и исследуемый интеграл сходится.
|
Пример 8. Исследовать на сходимость несобственный интеграл  .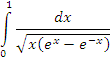
Решение. В окрестности особой точки x = 0 разность 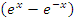 представляет собой бесконечно малую первого порядка по сравнению с x:
 .
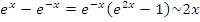 и интеграл расходится.
|
Пример 9. Исследовать на сходимость несобственный интеграл  .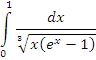
Решение. В окрестности особой точки x = 0 подынтегральная функция ведет себя как 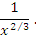 Следовательно, интеграл сходится.
|