. Исследовать на сходимость несобственный интеграл
в зависимости от значений параметра p > 0 (A> 1).
Решение. Представим подынтегральную функцию в виде

 .
Интеграл от первого члена в правой части этого равенства
сходится для всех значений p > 0 (см. Пример 1) и, таким образом, интегралы 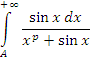 и и  сходятся или рассходятся одновременно. сходятся или рассходятся одновременно.
Рассмотрим интеграл  и выполним оценку его подынтегральной функции. и выполним оценку его подынтегральной функции.
-
Оценка со стороны больших значений:
 .
Поскольку
 ,
то интеграл  сходится при p > 1/2. сходится при p > 1/2.
Тогда по признаку сравнения при p > 1/2 сходится и интеграл  , что влечет за собой сходимость интеграла , что влечет за собой сходимость интеграла 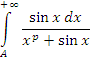 . .
-
Оценка со стороны меньших значений:

 .
Интеграл от  ведет себя так же, как интеграл от ведет себя так же, как интеграл от  , то есть сходится. Однако интеграл от , то есть сходится. Однако интеграл от  расходится при p ≤ 1/2. расходится при p ≤ 1/2.
Следовательно, интеграл 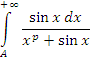 расходится, если p ≤ 1/2. расходится, если p ≤ 1/2.
|
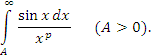
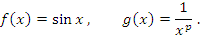
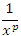 монотонно стремится к нулю при x → +∞. Следовательно, при p > 0 интеграл от произведения этих функций сходится на указанном промежутке.
монотонно стремится к нулю при x → +∞. Следовательно, при p > 0 интеграл от произведения этих функций сходится на указанном промежутке.
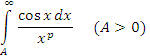
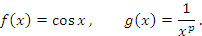
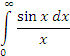

 ,
,
 и A > 0.
и A > 0.
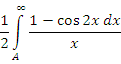
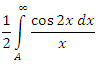
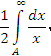
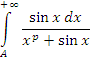

 .
.

 сходятся или рассходятся одновременно.
сходятся или рассходятся одновременно.
 .
.
 ,
,
 сходится при p > 1/2.
сходится при p > 1/2.

 .
.
 ведет себя так же, как интеграл от
ведет себя так же, как интеграл от  , то есть сходится. Однако интеграл от
, то есть сходится. Однако интеграл от  расходится при p ≤ 1/2.
расходится при p ≤ 1/2.