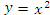 .
.
Решение. Абсциссы точек пересечения заданных линий являются пределами интегрирования и представляют собой решения уравнения
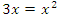 :
:
x1 = 0, и x2 = 3.
Тогда
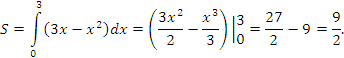
| Площадь плоской области |
Пример 1. Найти площадь области, заключенной между линиями y = 3x и 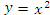 . .
Решение. Абсциссы точек пересечения заданных линий являются пределами интегрирования и представляют собой решения уравнения 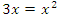 : :
x1 = 0, и x2 = 3. Тогда 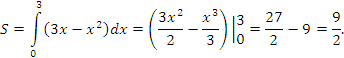
|
Пример 2. Найти площадь фигуры, ограниченной графиком функции 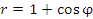 . .
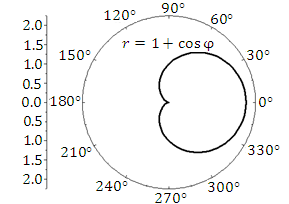
Рис. 1. Деления на окружности соответствуют значениям полярной координаты 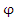 . Деления на вертикальной линии – значениям полярной координаты r. . Деления на вертикальной линии – значениям полярной координаты r.
Решение. 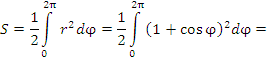
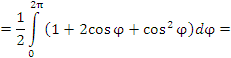
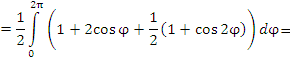
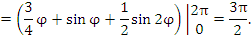
|
Пример 3. Найти площадь фигуры, ограниченной осью 0x и одной аркой циклоиды
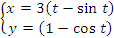
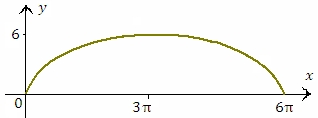  . .
Рис. 2. Первая арка циклоиды. Циклоида представляет собой линию, которую описывает точка на ободе катящегося без проскальзывания колеса. Решение. Представим интеграл 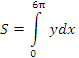 в терминах переменной t. в терминах переменной t.
Учитывая, что x(0)=0, 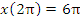 и и 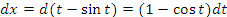 , получаем , получаем
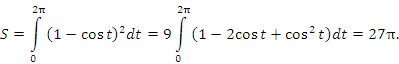
|
Пример 4. Найти площадь круга радиуса R.
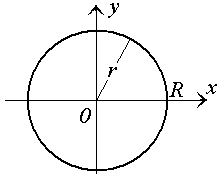 . .
Рис. 3. Окружность радиуса R Решение. Уравнение окружности 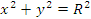 принимает наиболее простой вид при переходе к полярной системе координат: r = R. принимает наиболее простой вид при переходе к полярной системе координат: r = R.
Тогда 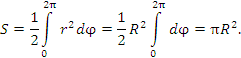
|
Пример 5. Найти площадь эллипса с полуосями a и b.
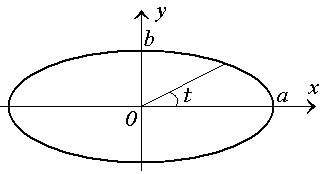
Рис. 4. Эллипс с полуосями a и b. Решение. Представим уравнение эллипса в параметрическом виде: 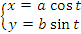
Найдем пределы интегрирования: x = – a при 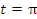 ; ;
x = a при t = 0. Учитывая, что dx = 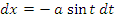 и меняя местами пределы интегрирования, вычисляем площадь: и меняя местами пределы интегрирования, вычисляем площадь:
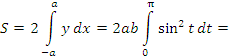
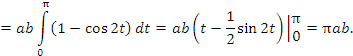
|
Пример 6. Вычислить площадь фигуры, заключенной между параболой 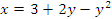 и осью ординат. и осью ординат.
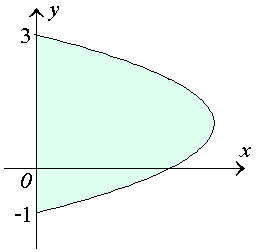
Рис. 5. Область, ограниченная параболой 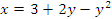 и осью ординат. и осью ординат.
Решение. Поскольку переменные x и y поменялись ролями, то площадь вычисляется по формуле 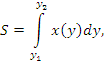
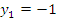 и и 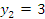 – точки пересечения параболы с осью ординат. – точки пересечения параболы с осью ординат.
Таким образом, 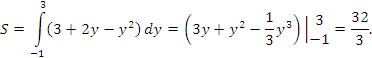
|