|
3. Выяснить сколько решений имеет система линейных уравнений, заданная расширенной матрицей

при различных значениях параметра a.
Решение. Если 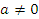 , то , то 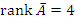 , тогда как , тогда как 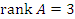 . В этом случае система является несовместной и не имеет решений. . В этом случае система является несовместной и не имеет решений.
Если a = 0, то 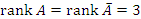 , что меньше числа неизвестных, количество которых равно 4. Тогда одна из неизвестных должна рассматриваться как свободный параметр, и при этом система имеет решение при любых значениях этого параметра. , что меньше числа неизвестных, количество которых равно 4. Тогда одна из неизвестных должна рассматриваться как свободный параметр, и при этом система имеет решение при любых значениях этого параметра.
Следовательно, система имеет бесконечное множество решений.
|