| Обобщенное правило Крамера |
|
1. Дана система линейных уравнений,
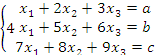
Решение. Составим расширенную матрицу и преобразуем ее к ступенчатой форме:
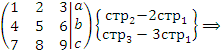
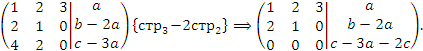
 , то система является несовместной. В противном случае одна из неизвестных является свободной переменной и, следовательно, система имеет бесконечное множество решений.
|
|
2. Система линейных уравнений задана расширенной матрицей, представленной в приведенно-ступенчатой форме:
Решение. Очевидно, что ранг матрицы, составленной из коэффициентов при неизвестных, равен рангу расширенной матрицы и совпадает с числом неизвестных. Следовательно, система уравнений имеет единственное решение – согласно следствию из обобщенного правила Крамера. |
|
3. Выяснить сколько решений имеет система линейных уравнений, заданная расширенной матрицей
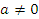Решение. Если  , то 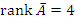 , тогда как  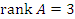. В этом случае система является несовместной и не имеет решений.
Если a = 0, то |
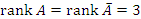, что меньше числа неизвестных, количество которых равно 4. Тогда одна из неизвестных должна рассматриваться как свободный параметр, и при этом система имеет решение при любых значениях этого параметра.