1. Решить систему уравнений
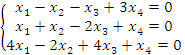
Решение. Выполним элементарные преобразования над строками матрицы коэффициентов, приведя ее к ступенчатому виду:
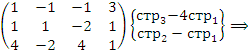
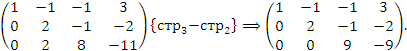
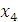 следует рассматривать как свободный параметр.
следует рассматривать как свободный параметр.
Далее нужно присвоить этому параметру произвольное значение
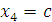 и выразить базисные неизвестные
и выразить базисные неизвестные 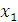 ,
, 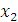 и
и 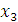 через c.
через c.
Преобразованная матрица соответствует следующей системе уравнений:
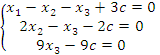
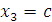 .
.
Выразим остальные базисные переменные:
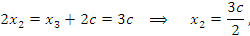
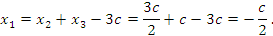
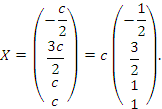
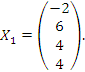
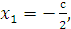
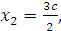
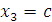
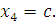
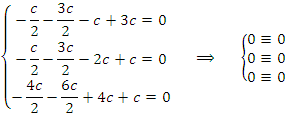
 .
.


 , а число неизвестных равно 4, то две неизвестные должны рассматриваться как базисные, а оставшиеся переменные как свободные параметры. Полагая
, а число неизвестных равно 4, то две неизвестные должны рассматриваться как базисные, а оставшиеся переменные как свободные параметры. Полагая  и
и  , получаем уклрлченную систему уравнений
, получаем уклрлченную систему уравнений

 ,
,  .
.



 образуют фундаментальную систему решений.
образуют фундаментальную систему решений.
 и
и  .
.



 . Решить однородную систему линейных уравнений AX = 0.
. Решить однородную систему линейных уравнений AX = 0.



 .
.