|
3. Решить систему уравнений
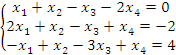
методом Гаусса.
Решение. Производя элементарные преобразования над строками, приведем расширенную матрицу к ступенчатой форме:
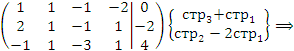
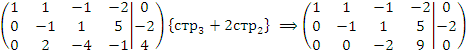
Выпишем соответствующую систему уравнений:
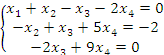
Последнее уравнение содержит две переменных, одну из которых нужно рассматривать в качестве свободного параметра. Назначим этому параметру произвольное значение 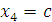 и выразим остальные переменные через c: и выразим остальные переменные через c:
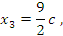
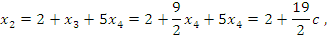
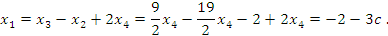
Таким образом, общее решение системы имеет вид
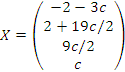
Если подставить вместо c произвольное число, например нуль, то мы получим частное решение: 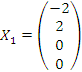 . .
Подставляя c = 2, получаем другое частное решение: 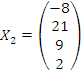 . .
Таким образом, данная система имеет бесконечное множество решений.
Проверка: Подставим 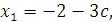 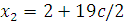 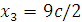 и и 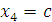 в каждое уравнение системы: в каждое уравнение системы:

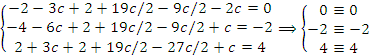
Уравнения обратились в тождества.
|