Основная
идея метода Гаусса при решении системы линейных уравнений заключается в следующем:
-
Системе линейных уравнений ставится в соответствие матрица, элементарные преобразования которой эквивалентны преобразованиям системы уравнений.
В результате таких преобразований матрица, соответствующая равносильной системе уравнений, имеет более простой вид и, следовательно, более простой вид принимают уравнения системы.
-
Целью таких преобразований является получение матрицы с максимально возможным числом нулевых элементов, что означает исключение неизвестных из ряда уравнений системы.
-
Следует ориентироваться на то, чтобы каждое элементарное преобразование обращало в нуль какой-либо элемент матрицы и при этом не изменяло все те нулевые элементы, которые были получены при всех предыдущих преобразованиях.
-
Другим ориентиром является стремление сделать равным единице определенный элемент матрицы и при этом не изменить все те единичные элементы, которые были получены при всех предыдущих преобразованиях.
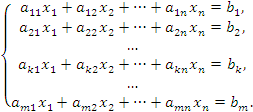
 .
.
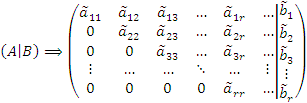 ,
,
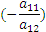 , к третьей строке - первую, умноженную на
, к третьей строке - первую, умноженную на 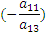 и так далее.
и так далее.
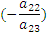 , к третьей строке - первую, умноженную на
, к третьей строке - первую, умноженную на 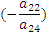 и так далее.
и так далее.