AX = B,
эквивалентно системе обычных уравнений.Если, например, A и B - числовые матрицы n-го порядка, X - матрица n-го порядка, составленная из неизвестных, то матричное уравнение AX = B описывает систему n2 уравнений с n2 неизвестными.
|
|
| Основные понятия |
|
|
|
|
|
Равенство матриц влечет за собой попарное равенство соответствующих матричных элементов. Поэтому матричное уравнение
AX = B, эквивалентно системе обычных уравнений.Если, например, A и B - числовые матрицы n-го порядка, X - матрица n-го порядка, составленная из неизвестных, то матричное уравнение AX = B описывает систему n2 уравнений с n2 неизвестными. |
|
Рассмотрим систему m линейных уравнений с n неизвестными:
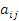 – числовые коэффициенты; – числовые коэффициенты; 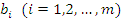 – свободные члены; – свободные члены; 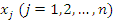 – неизвестные. – неизвестные.
Решением системы (1) является совокупность значений неизвестных Система (1) может быть представлена в виде матричного уравнения AX = B, где A – матрица, составленная из коэффициентов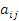 при неизвестных; матрица B представляет собой столбец свободных членов; элементами матрицы X являются
неизвестные при неизвестных; матрица B представляет собой столбец свободных членов; элементами матрицы X являются
неизвестные 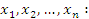
AX = 0. Две системы уравнений, имеющие одинаковые множества решений, называются эквивалентными.Очевидно, что такие операции как перестановка уравнений местами, умножение обеих частей уравнения на ненулевое число или прибавление к одному уравнению другого, умноженного на некоторое число, преобразуют систему уравнений в ей эквивалентную. |