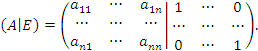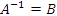Вычисление обратной матрицы методом элементарных преобразований

Вычисление обратной матрицы методом элементарных преобразований

      Метод вычисления обратной матрицы, основанный на построении присоединенной матрицы, становится крайне неэффективным, как только речь заходит о матрицах достаточно высокого порядка.
      В таких случаях следует отдавать предпочтение методу Гаусса.

      Любую несингулярную матрицу A можно преобразовать в единичную матрицу, выполняя над ее строками элементарные преобразования.

      Если некоторые операции преобразуют матрицу A в единичную, то для нахождения обратной матрицы достаточно выполнить эти же самые преобразования над единичной матрицей.

Предположим, что матрица A - неособенная и рассмотрим метод нахождения обратной матрицы, основанный на элементарных операциях над строками.

В данном контексте под элементарными преобразованиями понимается:

Умножение строки на любое ненулевое число.
Прибавление к одной строке любой другой, предварительно умноженной на любое число.

Алгоритм метода чрезвычайно прост по своей сути.

Сначала составляется расширенная матрица – присоединением к матрице A единичной матрицы E:

Затем с помощью элементарных операций над строками расширенная матрица (A | E) преобразуется к виду (E | B).

С формальной точки зрения такие преобразования могут быть реализованы умножением на матрицу A некоторой матрицы T, которая представляет собой произведение соответствующих элементарных матриц (матрицы перестановки, матрицы масштабирования, неунитарной матрицы):

TA = E.

Это уравнение означает, что матрица преобразования T представляет собой обратную матрицу для матрицы A:

T = A^-1.

Тогда TE = A^-1 и, следовательно,