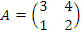 .
.
Решение. Вычислим определитель матрицы:
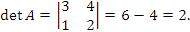
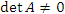 , то обратная матрица существует.
, то обратная матрица существует.
Далее найдем алгебраические дополнения всех элементов:
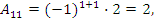
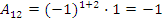 ,
,
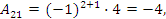
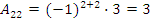 .
.
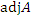 :
:
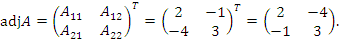
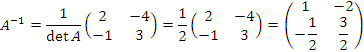
Проверка
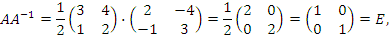
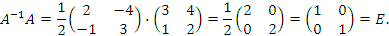
| Теорема об обратной матрице |
1. Найти обратную матрицу для матрицы 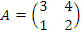 . .
Решение. Вычислим определитель матрицы:
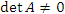 , то обратная матрица существует. , то обратная матрица существует.
Далее найдем алгебраические дополнения всех элементов:
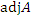 : :
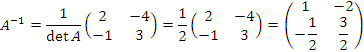
Проверка 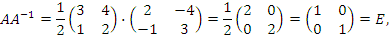
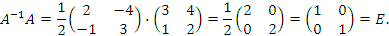
|
2. Найти обратную матрицу для матрицы 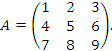
Решение. Вычисляем определитель: 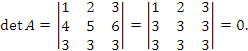
Матрица A является сингулярной и, следовательно, обратная матрица не существует. |
|
3. Найти обратную матрицу для матрицы
2) Найдем алгебраические дополнения элементов матрицы:
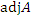 : :
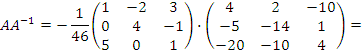
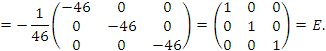
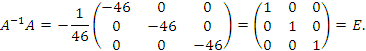
|
|
3. Даны матрицы 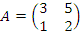 и и 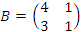 . Решить матричное уравнение . Решить матричное уравнение
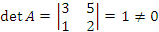 , то матрица A является неособенной и существует обратная матрица , то матрица A является неособенной и существует обратная матрица 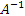 . .
Умножим обе части уравнения (*) на матрицу 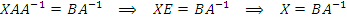
Составим присоединенную матрицу 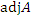 : :
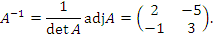
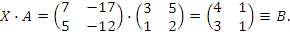
|