В этом разделе вводится терминология, сопутствующая понятию обратной матрицы.
|
|
| Основные понятия |
|
|
|
|
Рассмотрим квадратную матрицу A. Напомним, что матрица 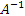 называется обратной матрицей, если называется обратной матрицей, если
Отметим, несколько забегая вперед, что условием существования обратной матрицы является отличие от нуля определителя матрицы. В этой связи уместно ввести соответствующую терминологию. Матрица называется сингулярной, если ее определитель равен нулю. В качестве синонимов используются также термины “особая матрица” или “вырожденная матрица”.
Если
Если в матрице A заменить ее элементы их алгебраическими дополнениями и транспонировать матрицу, то полученная матрица называется присоединенной для A и обозначается символическим выражением
Таким образом, |