Доказательство


	Разложение определителя по элементам строки или столбца

Теорема.

Доказательство. По определению, детерминант матрицы A представляет собой сумму

(*)

по всем возможным перестановкам индексов, нумерующих столбцы.

Выберем произвольным образом некоторую строку, например, с номером i.
Один из элементов этой строки представлен в каждом произведении . Поэтому слагаемые суммы (*) можно перегруппировать, объединив в первую группу те, что содержат элемент a₁₁ в качестве общего множителя, во вторую группу – члены, содержащие элемент a₁₂ и т.д.
Другими словами, выражение (*) можно представить в виде линейной комбинации элементов a_{i j} (j = 1,2,…,n):

где

Покажем, что

представляет собой алгебраическое дополнение элемента a_{i j}.
Перестановка

преобразуется в перестановку

посредством (i – 1) транспозиций элемента j с соседними элементами. В полученной перестановке элемент j образует (j – 1) инверсий с другими элементами.
Следовательно,

Однако сумма

представляет собой минор элемента a_{i j} .
Таким образом,

и, следовательно, представляет собой алгебраическое дополнение элемента a_{i j}.

Поскольку 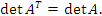, то тем самым доказана и Теорема о разложении определителя по элементам столбца.

Закрыть окно