Свойство 1. Определитель транспонированной матрицы равен определителю исходной матрицы: 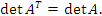 .
.
 (1)
(1)
| Свойства определителей |
|
Свойство 1. Определитель транспонированной матрицы равен определителю исходной матрицы:
|
|
Свойство 2. Умножение всех элементов строки или столбца определителя на некоторое число λ равносильно умножееию определителя на это число: 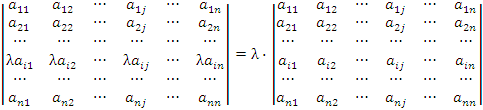 . .
Доказательство. При умножении строки (или столбца) определителя на число λ один из сомножителей в произведении  умножается на это число. В результате число λ является общим множителем суммы (1), представляющей собой определение детерминанта матрицы A. умножается на это число. В результате число λ является общим множителем суммы (1), представляющей собой определение детерминанта матрицы A.
|
|
Свойство 3. Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный. Доказательство. По Теореме 1, любая транспозиция изменяет четность перестановки. Следовательно, при перестановке двух строк (столбцов) каждое слагаемое суммы (1) изменяет свой знак на противоположный. |
|
Свойство 4. Если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю. Доказательство. Каждая строка и каждый столбец матрицы A представлены одним из своих элементов в произведении . Следовательно, сумма (1) содержит только нулевые слагаемые. . Следовательно, сумма (1) содержит только нулевые слагаемые.
|
|
Свойство 5. Если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен нулю. Доказательство. По Свойству 3, при перестановке двух строк местами определитель изменяет свой знак. С другой стороны, перестановка местами одинаковых строк не изменяет определитель. Следовательно, det A = –det A, что влечет det A = 0. |
|
Свойство 6. Если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю. Доказательство. Общий множитель строки можно вынести за знак определителя. Полученный при этом определитель имеет две одинаковых строки. Согласно Свойству 5 такой определитель равен нулю. |
|
Свойство 7. Определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали: 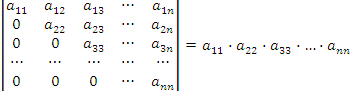 . .
Доказательство. По определению (1), det A представляет собой алгебраическую сумму произведений элементов (с учетом правила выбора знаков), составленных таким образом, чтобы каждая строка и каждый столбец матрицы A были представлены в произведении одним и только одним элементом. В первом столбце имеется только один ненулевой элемент, а именно a11. Второй столбец вносит ненулевой вклад в произведение только при выборе элемента a22, поскольку первая строка уже представлена своим элементом. Аналогично, в третьем столбце выбор может быть остановлен только на элементе a33 и так далее. Таким образом, сумма (1) содержит только один ненулевой член, который равен произведению элементов, стоящих на главной диагонали. |
|
Свойство 8. Если все элементы k-ой строки (столбца) определителя представлены в виде сумм ak j + bk j, то определитель можно представить в виде суммы соответствующих определителей:
|
|
Свойство 9. Определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и тоже число.
|