Определитель числовой матрицы представляет собой некоторое число. Определителем функциональной матрицы является некоторая функция.
Оказывается, что если определитель матрицы равен нулю, то по крайней мере одна из ее строк (или один из ее столбцов) является линейной комбинацией остальных строк (столбцов). Другими словами, строка (столбец) матрицы может быть представлена в виде суммы других строк (столбцов), предварительно умноженных на числовые коэффициенты.
Если же определитель матрицы не равен нулю, то строки матрицы являются линейно независимыми.
|
Пусть A = || ai j || – произвольная
квадратная матрица n-го порядка, и пусть 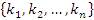 – некоторая перестановка упорядоченного множества – некоторая перестановка упорядоченного множества 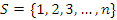 первых n натуральных чисел. первых n натуральных чисел.
Составим произведение
| |
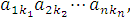
|
(1) |
|
содержащее n элементов, в котором каждая строка и каждый столбец матрицы A представлены одним и только одним из своих элементов. Например, первый сомножитель в этом произведении является элементом первой строки и k1-го столбца, второй сомножитель представляет вторую строку и k2-ой столбец и так далее.
Согласно Теореме 2, существует n! различных перестановок 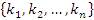 , каждой из которых соответствует произведение вида (1) и, следовательно, существует n! различных произведений такого типа. , каждой из которых соответствует произведение вида (1) и, следовательно, существует n! различных произведений такого типа.
Сопоставим каждому из полученных произведений знак плюс или минус – в зависимости от четности или нечетности перестановки 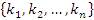 . .
Чтобы формально описать такое сопоставление, введем число инверсий в перестановке 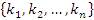 , которое обозначим символическим выражением , которое обозначим символическим выражением  . .
Заметим, что
| |

|
(2) |
|
Алгебраическая сумма всех возможных произведений вида
| |
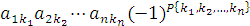
|
(3) |
|
называется (или ) матрицы A:
| |

|
(4) |
|
Для записи определителя используется также обозначение в виде массива матричных элементов в вертикальных скобках:
| |

|
(5) |
|
Представляется уместным отметить некоторые важные обстоятельства, относящиеся к понятию определителя матрицы:
-
В формуле (4), выражающей собой определение det A, строки и столбцы матрицы A представлены равноправно. Лишь для удобства изложения первый элемент в произведении (3) выбирался из первой строки, второй элемент – из второй строки и так далее. В результате суммирования по всем возможным перестановкам индексов, нумерующих столбцы, выражение (4) включает в себя все произведения рассматриваемого типа, представленные в определенной последовательности.
Формальное равноправие строк и столбцов в определении det A можно выразить следующим эквивалентным выражением:
| |
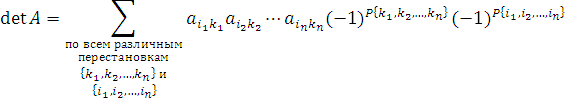 . .
|
(6) |
|
-
Число четных перестановок
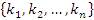 в сумме (4) совпадает с числом нечетных перестановок и равно в сумме (4) совпадает с числом нечетных перестановок и равно 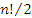 . .
-
Определитель является одной из важнейших характеристик матрицы. При этом наиболее существенным часто оказывается не его конкретное числовое значение, а сам факт его равенства нулю или отличия от нуля. Например, матрица A имеет обратную лишь в том случае, когда
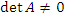 (что будет доказано в одном из ближайших разделов). (что будет доказано в одном из ближайших разделов).
-
Не следует путать определитель матрицы с самой матрицей: Матрица представляет собой массив чисел, тогда как определителем матрицы является одно единственное число.
|
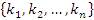 – некоторая перестановка упорядоченного множества
– некоторая перестановка упорядоченного множества 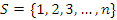 первых n натуральных чисел.
первых n натуральных чисел.
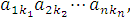
 .
.

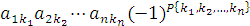


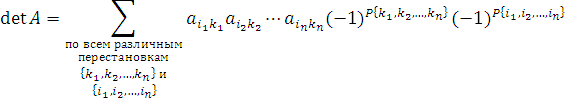 .
.
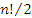 .
.
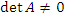 (что будет доказано в одном из ближайших разделов).
(что будет доказано в одном из ближайших разделов).