Этот раздел фактически представляет собой словарик терминов, за каждым из которых закреплены некоторые свойства матриц.
Эти определения следует просто осмыслить и запомнить.
Примерно также как мы запомнили в свое время смыслы терминов "гулять, есть" и так далее.
|
Говорят, что матрица имеет треугольный вид, если все ее элементы,
расположенные выше или ниже главной диагонали, равны нулю:
 или 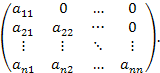 Рис.1
Рис.1. Верхняя треугольная матрица и нижняя треугольная матрица.
Треугольные матрицы обладают следующими свойствами:
-
Сумма треугольных матриц одного наименования есть треугольная матрица того же наименования; при этом диагональные элементы матриц складываются.
-
Произведение треугольных матриц одного наименования есть треугольная матрица того же наименования.
-
При возведении треугольной матрицы в целую положительную степень ее диагональные элементы возводятся в эту же самую степень.
-
При умножении треугольной матрицы на некоторое число ее диагональные элементы умножаются на это же самое число.
Доказательство утверждений предоставляется читателю.
|
|
Если в произвольной m × n матрице 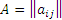 произвести взаимную замену строк и
столбцов, то полученная матрица называется транспонированной и
обозначается символом произвести взаимную замену строк и
столбцов, то полученная матрица называется транспонированной и
обозначается символом 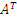 . Другими словами, строки матрицы A являются столбцами матрицы . Другими словами, строки матрицы A являются столбцами матрицы
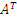 , а столбцы матрицы A являются строками матрицы , а столбцы матрицы A являются строками матрицы
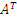 :
Очевидно, что :
Очевидно, что
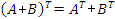 ,
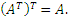
Операция транспонирования произведения матриц обладает следующим свойством:
|
|
Квадратная матрица A называется симметричной, если 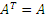 ,
что означает ,
что означает 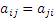 . .
Матрица называется кососимметричной, если 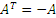 , то есть , то есть
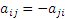 . .
|
|
 или
или 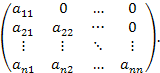
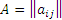 произвести взаимную замену строк и
столбцов, то полученная матрица называется транспонированной и
обозначается символом
произвести взаимную замену строк и
столбцов, то полученная матрица называется транспонированной и
обозначается символом 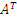 . Другими словами, строки матрицы A являются столбцами матрицы
. Другими словами, строки матрицы A являются столбцами матрицы
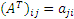
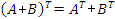 ,
,
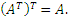
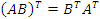
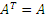 ,
что означает
,
что означает 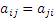 .
.
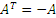 , то есть
, то есть
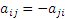 .
.