.
Пусть A, B и C – квадратные матрицы одного и того же порядка.
Если существуют обратные матрицы A –1, B –1 и C –1, то существует и обратная матрица для произведения ABC, причем
(ABC)–1 = C –1 B –1 A –1.
Действительно,
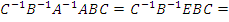
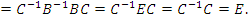
Аналогично,
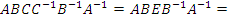
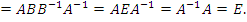
|
***
.
Пусть 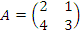 . .
Проверить прямым вычислением, что матрица
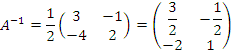
является обратной матрицей.
Решение
Вычислим произведение A –1A :
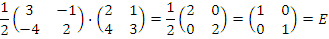
Такой же результат справедлив для произведения AA –1 :
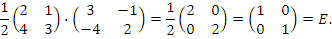
|
|