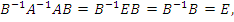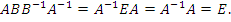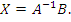Однако матричные произведения A B-1 и B-1A не обязательно совпадают между собой. И это означает, что операция деления одной матрицы на другую - если бы такая операция была введена - не может интерпретироваться однозначно. Поэтому вместо одной операции деления матриц необходимо ввести целых две операции: умножением одной из этих матриц на обратную матрицу другой - слева или справа.
Ключевая формула, лежащая в основе определения обратной матрицы, выглядит также, что и в случае алгебры чисел:
A-1A = AA-1 = E,
где E - единичная матрица.
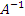 называется
называется 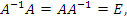
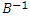 , то существует и обратная матрица для произведения AB, причем
, то существует и обратная матрица для произведения AB, причем
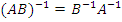 .
.