Диагональные матрицы (примеры)  
Пример 1.
Доказать, что произведение диагональных матриц есть диагональная матрица.

Доказательство:

Пусть 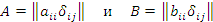– произвольные диагональные матрицы  n-го порядка. Рассмотрим  i,j-ый элемент матричного произведения AB:

.
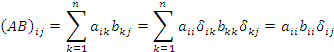Выражение в правой части этого равенства представляет собой матричный элемент диагональной матрицы.


***
Пример 2.
Доказать, что коммутатор диагональных матриц равен нулю.

Доказательство:

Пусть 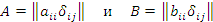– произвольные диагональные матрицы  n-го порядка. Рассмотрим  i,j-ый элемент матричного произведения BA:

.
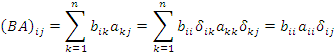Учитывая, что произведение диагональных матриц есть диагональная матрица (см Пример 1), заключаем, что произведение диагональных матриц коммутативно:  AB = BA.

***
Пример 3.
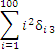Сумма    содержит только одно ненулевое слагаемое, поскольку  δi 3 = 1  при  i = 3  и  δi 3 = 0  для всех других значений  i.
Следовательно,

***
Пример 4.
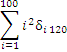Сумма    содержит только нулевые слагаемые, поскольку  δi 120 = 0  для всех  1 ≤ i ≤ 100.
Следовательно,

***
Пример 5.