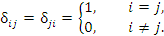Диагональные матрицы  
Некоторые матрицы специального вида обладают дополнительными и только им присущими свойствами. Такие матрицы принято наделять именами, которые в какой-то мере отражали бы их структуру. В частности, квадратные матрицы потому и называются квадратными, что они квадратные .

Например, диагональная матрица не изменится, если ее строки объявить столбцами (при этом ее столбцы автоматически становятся строками). Поэтому для диагональных матриц  A  и  B  исчезает неравноправие между строками и столбцами в произведении таких матриц и, следовательно,  AB = BA.

У каждого элемента, расположенного на главной диагонали квадратной матрицы, номер строки совпадает с номером столбца. Все другие матричные элементы ai j (i ≠ j) диагональной матрицы A равны нулю.

Подобные ситуации встречаются достаточно часто и поэтому договорились использовать для их описания специально введенное выражение вида δi j :

δi j = 1, если i = j,
δi j = 0, если i ≠ j.
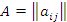Вот примерно такова логика изложения в данном разделе!

      В квадратной матрице элементы 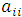( i = 1, 2, ..., n ) образуют главную диагональ и называются диагональными элементами. Главная диагональ проходит из левого верхнего угла матрицы в ее правый нижний угол.

   (1)  

      Совокупность элементов, расположенных на диагонали, проходящей из правого верхнего угла в левый нижний угол, называется побочной диагональю.

      Матрица , все внедиагональные элементы которой равны нулю, называется диагональной. Другими словами, элементы диагональной матрицы удовлетворяют условиям

   (2)  

      Для записи подобных выражений удобно использовать дельта-символ Кронекера, определяемый формулой

   (3)  

      Очевидно, что дельта-символ симметричен относительно перестановки индексов:

  δi j = δj i .  (4)  

      Другое важное свойство дельта-символа  δi j  заключается в том, что он снимает суммирование в выражениях вида

   (5)  
      В частности,
   (6)  

      В этих обозначениях формула (2) принимает вид
   (7)  

      Очевидно, что при умножении прямоугольной матрицы A справа на диагональную матрицу с диагональными элементами λ1, λ1, ..., λn первый столбец матрицы A умножается на число λ1 , второй - на число λ2 и так далее.
      При умножении матрицы A слева на такую диагональную матрицу каждая строка матрицы A умножается на соответствующее число λi.

      Диагональная квадратная матрица с равными диагональными элементами называется скалярной.