Во всех случаях, когда вводятся новые математические объекты, необходимо договариваться о правилах действий над ними, а также определить - какие объекты считаются равными между собой.
Природа объектов не имеет никакого значения. Это могут быть вещественные или комплексные числа, векторы, матрицы, строки или что-то иное.
К числу стандартных действий относятся линейные операции, а именно: умножение на число и сложение; в данном конкретном случае - умножкние матрицы на число и сложение матриц.
При умножении матрицы на число каждый матричный элемент умножается на это число, а сложение матриц подразумевает попарное сложение элементов, расположенных в эквивалентных позициях.
Терминологическое выражение "линейная комбинация" (векторов, матриц, строк, столбцов и так далее) всегда означает одно и тоже: алгебраическая сумма этих векторов (или матриц, строк, столбцов и так далее), предварительно умноженных на числовые коэффициенты.
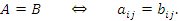
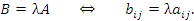
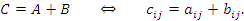
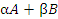 , где
, где 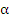 и
и 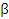 – числовые коэффициенты.
– числовые коэффициенты.