|
Let a function f (x) be defined
and continuous on a closed interval [a,
b] and be differentiable at each point of the open interval
(a, b). |
such that 
.The idea of a Proof is evident from the drawing.
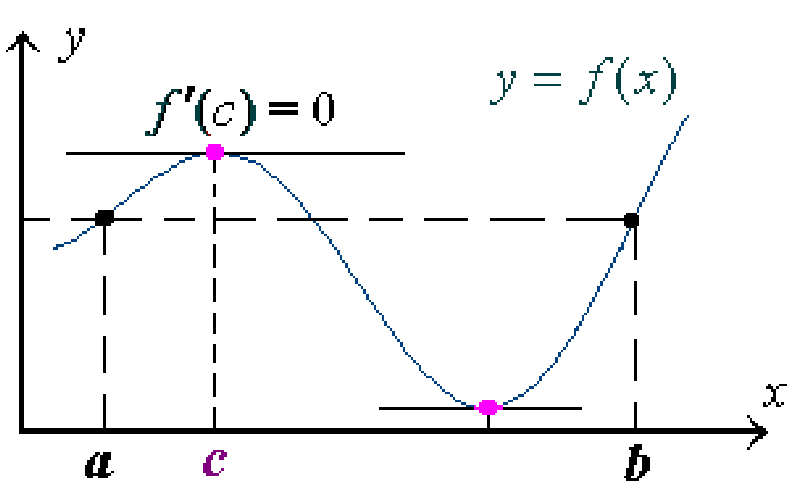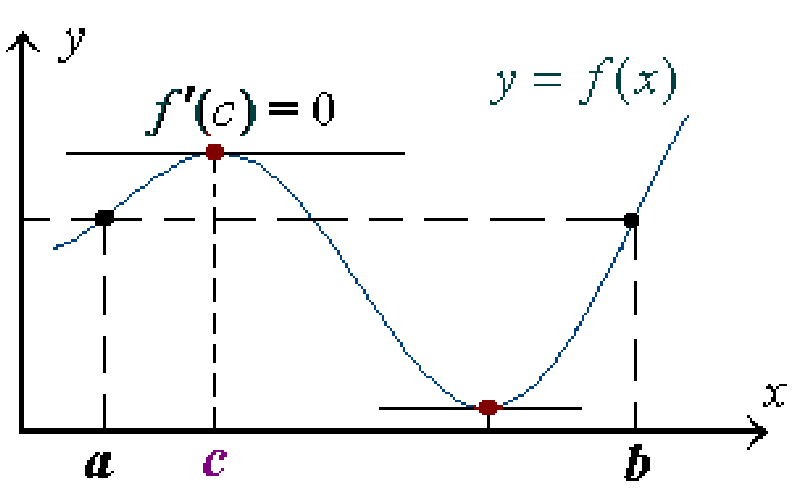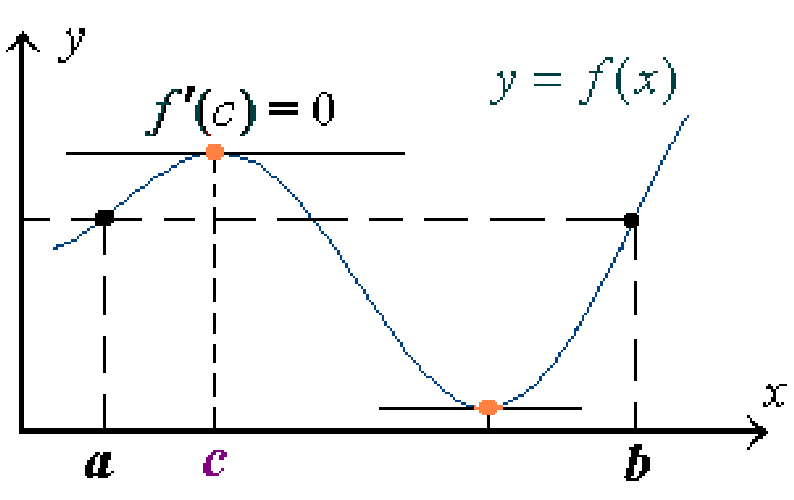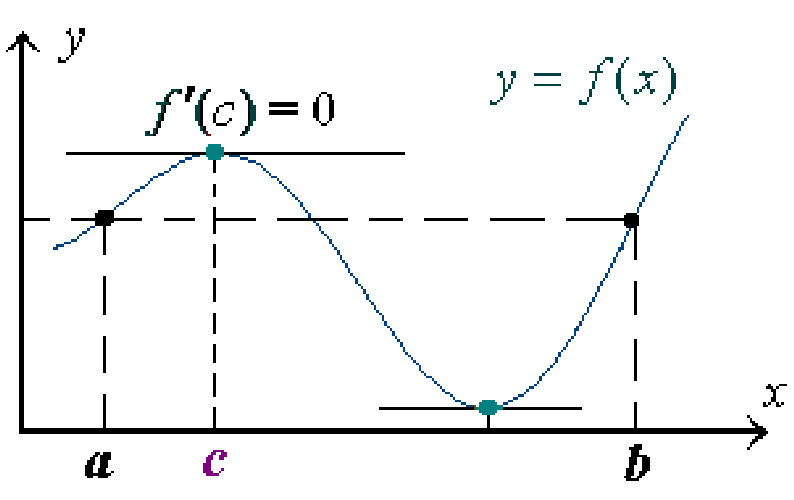
By assumption, the function f (x) is
continuous on the closed interval [a, b]
and f(a) = f (b), so f (x)
attains either its maximum or minimum at some point x
= c of the open interval (a,b). The
tangent line of the function 
at this point is a horizontal line.
Hence, its slope is equal to zero, that is, the derivative 
.
Note that the Rolle Theorem does not claim where c
can be found on (a, b). It claims only that
there exists at least one point c such that
.
As for the curve in the above drawing, there are two points satisfying
the equation 
.
