Let AB be the secant line, passing through
the points ![]() and
and ![]() . If
. If ![]() , that is,
, that is, ![]() approaches zero, then the secant
line approaches the tangent line at the point
approaches zero, then the secant
line approaches the tangent line at the point ![]() . Accordingly, the slope of the tangent
line is the limit of the slope of the secant line when
. Accordingly, the slope of the tangent
line is the limit of the slope of the secant line when ![]() approach zero:
approach zero:
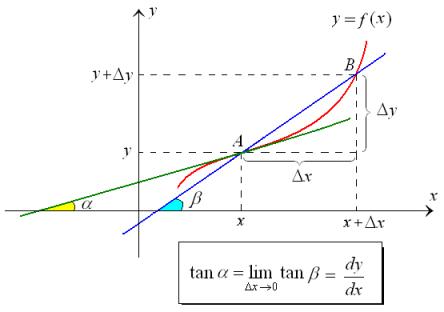
Thus, the derivative ![]() can be interpreted as the slope of
the tangent line at the point
can be interpreted as the slope of
the tangent line at the point ![]() on the graph of the function
on the graph of the function ![]() .
.
If a function is increasing on some interval, then the slope of the tangent is positive at each point of that interval, and hence, the derivative of the function is positive.
If a function is decreasing on some interval, then the slope of the tangent is negative at each point of that interval, and hence, the derivative of the function is negative.
If a function is increasing on some interval, then the slope of the tangent is positive at each point of that interval, and hence, the derivative of the function is positive.

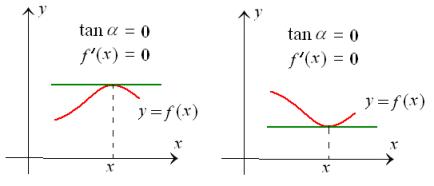
If a curve y = f (x) has a smooth top then
the peak of the curve serves as the boundary between intervals of increasing
and decreasing of the function. At this point the tangent is parallel
to the x-axis. Therefore, its slope equals
zero, and so ![]() .
.
Likewise, if a curve y = f (x) has a smooth
bottom then there exists a point peak of the curve serves as the boundary
between intervals of increasing and decreasing of the function. At this
point the tangent is parallel to the x-axis.
Therefore, its slope equals zero, and so ![]() .
.