| Example 1 |
Evaluate ![]() .
.
Solution: By the properties of limits,
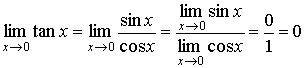 .
.
| Example 2 |
Evaluate 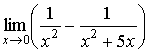 .
.
Solution: This indeterminate
form ![]() can be reduced to the form
can be reduced to the form ![]() , which is easily evaluated:
, which is easily evaluated:
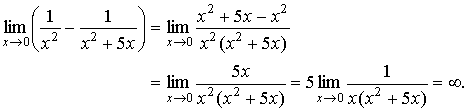
| Example 3 |
Find 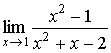 .
.
Solution: We cannot
substitute zero for x, since the expression
under the sign of the limit is an indeterminate form ![]() . It is necessary to transform the expression
and reduce the common infinitesimal factors:
. It is necessary to transform the expression
and reduce the common infinitesimal factors:
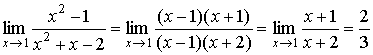 .
.
| Example 4 |
Evaluate 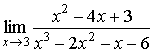 .
.
Solution: Using the same idea as above we obtain
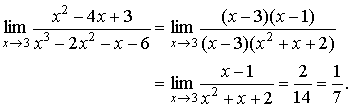
| Example 5 |
Find
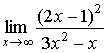
Solution: In order
to evaluate the indeterminate form ![]() , divide the numerator and denominator
of the given expression by x2
and then apply the properties of limits:
, divide the numerator and denominator
of the given expression by x2
and then apply the properties of limits:
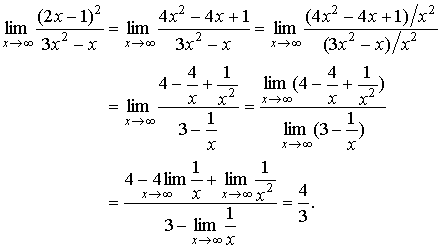
Short solution: Infinite function ![]() is equivalent to
is equivalent to ![]() as
as ![]() , while
, while ![]() . Therefore,
. Therefore,
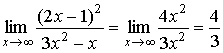 .
.
| Example 6 |
Evaluate 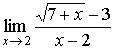 .
.
Solution: To evaluate
the indeterminate form ![]() , multiply the numerator and denominator
by factor
, multiply the numerator and denominator
by factor ![]() to compete the difference between two
squares. Then reduce the common infinitesimal factors:
to compete the difference between two
squares. Then reduce the common infinitesimal factors:
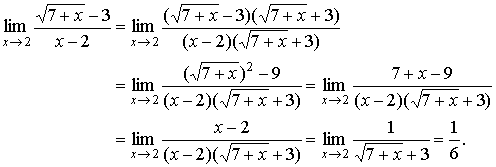
| Example 7 |
Evaluate 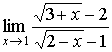 .
.
Solution: Likewise the above, we need to reduce the common infinitesimal factor. Note that
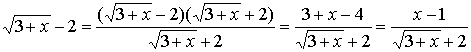
and
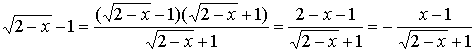 .
.
Therefore,
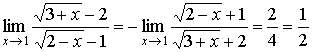 .
.
| Example 8 |
Evaluate 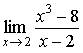 .
.
Solution: Using the formula of the difference between two cubes, factor the numerator and reduce the common multipliers of the numerator and denominator:
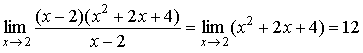 .
.
