| Example 1 |
Functions 
and 
are equivalent infinitesimal functions
as 
:
.
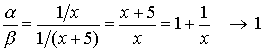Therefore, 
can be substituted for 
in expressions under the sign of the
limit as 
. For instance,
and
.
Therefore,
.
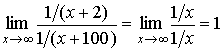| Example 2 |
 |
Infinitesimal functions 
and 
have the same order as 
:
.
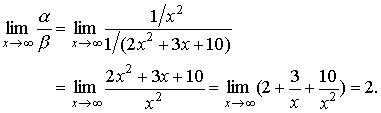Therefore, 
as 
, that is, 
can be substituted for 
in expressions under the sign of the
limit as 
. For instance,
and
.
Hence,
.
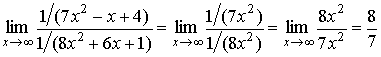| Example 3 |
|
Each of infinitesimal functions
has a higher order of smallness with respect to x as 
.
Therefore,
,
that is, each of the functions, 
, is a negligible quantity with respect
to x as 
.
| Example 4 |
 |
Infinitesimal functions 
and 
are equivalent as 
, since
.
The difference between them is an infinitesimal function of a higher order of smallness:
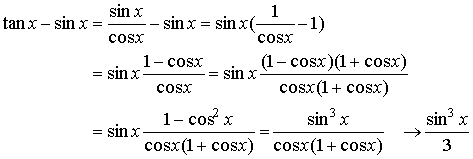
as 
.
Since
,
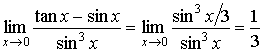is an infinitesimal function of the
third order with respect to 
as 
.
