| Example 6 |
Given infinitesimal functions 
and 
as 
, find the limit of their ratio.
Solution:
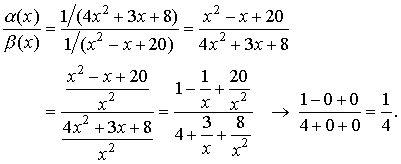
The limit is a finite number.
Therefore, 
and 
are infinitesimal functions of the same
order as 
.
| Example 7 |
 |
Given infinitesimal functions 
and 
as 
, find the limit of their ratio.
Solution:
.
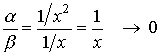The limit is equal to zero. Therefore, 
is an infinitesimal function of a higher
order of smallness to 
as 
, and 
is an infinitesimal function of a lower
order with respect to 
.
Since
,
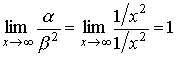which is a finite number, then, 
is an infinitesimal function of the
second order with respect to 
as 
.
