| Example 1 |
The sequence
![]()
is infinitesimal, since
![]() as
as ![]() .
.
Formal Proof: We
need to show that for any ![]() there exists a number N
such that the inequality
there exists a number N
such that the inequality ![]() implies
implies
![]() .
.
Let integer N be greater than or equal to
![]() .
.
Then inequality
![]() implies
implies ![]() ,
,
which means
![]()
for any arbitrary small ![]() .
.
Hence, the desired statement.
If we set ![]() then
then ![]() for all
for all ![]() .
.
Therefore, all terms of the sequence are in the given delta vicinity of zero with the exception of the first hundred of the terms.
If ![]() then
then ![]() for all
for all ![]() .
.
Therefore, all terms of the sequence are in the delta vicinity of zero with the exception of the first thousand of the terms.
It does not matter how many terms are not in the delta vicinity. It is only important that a finite number of terms is outside of any neighborhood of zero.
| Example 2 |
The variable ![]() is infinitesimal, since
is infinitesimal, since
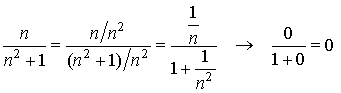
as ![]() .
.
Formal Proof: First, transform the general term as follows:
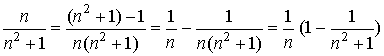 .
.
Next, if we set
![]() ,
,
then for any ![]() inequality
inequality ![]() implies
implies ![]() , which means
, which means ![]() .
.
However,
![]() .
.
Therefore,
![]()
![]()
![]()
![]()
![]()
for any arbitrary small and positive ![]() .
.
Hence, the desired result.
| Example 3 |
The variable ![]() is infinitesimal, because
is infinitesimal, because
![]()
as ![]() .
.
Formal Proof: Given any arbitrary small and positive
![]()
![]()
![]()
![]()
![]() .
.
Hence, we can set
![]() ,
,
and so inequality ![]() implies
implies
![]()
for any arbitrary small ![]() .
.
| Example 4 |
The variable ![]() is infinitesimal, because
is infinitesimal, because
![]()
as ![]() .
.
Formal Proof: Given any arbitrary small and positive
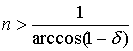
![]()
![]()
![]()
![]()
![]()
![]() .
.
Let integer N be greater than or equal to
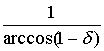 .
.
Then inequality ![]() implies
implies
![]()
for any arbitrary small ![]() .
.
