|
A numerical sequence
is a set of ordered values of a function, whose domain consists
of the set of all natural numbers in ascending order of the numbers.
|
The elements of a sequence are called the terms.
The n-th term of a sequence is called the general term or variable of the sequence. The general term is denoted by a lower case letter with the subscript n:
, 
, 
, 
, 
, 
, etc.
Usually, index n takes on values 1, 2, 3, ...
A numerical sequence is completely determined by its general term. To denote a sequence, we use the general term in braces:
, 
, 
, etc.
| Graphic Presentation of Sequences |
 |
By the Number Line:
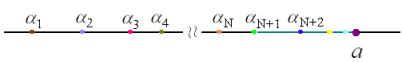
By Two-Dimensional Chart:
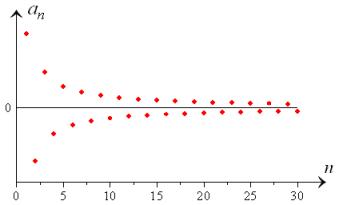
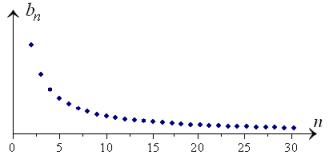
Examples of Sequences:
The elements of an arithmetical progression
are the terms of a numerical sequence with the general term 
:
The general term 
determines the sequence
The sequence
has the general term
.
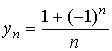| Bounded and Unbounded Sequences |
|
|
A sequence for each natural number n. |
is called an 
Any nonempty upper-bounded sequence has the least upper bound.
|
A sequence for each natural number n. |
is called a 
Each nonempty lower-bounded sequence has the greatest lower bound.
A bounded sequence has an upper bound and a lower bound at the same time. Otherwise, a sequence is unbounded.
| Monotone Sequences |
|
|
A sequence for each natural number n. |
is called 
|
A sequence for each natural number n. |
is called a 
