|
The scalar product and the vector product may be combined into the scalar triple product (or mixed product): |
| Theorem |
Let ![]() ,
, ![]() and
and ![]() . Then the scalar triple product
is given by the formula
. Then the scalar triple product
is given by the formula
 .
.
The proof is straightforward. Carrying out the scalar product of the vectors
![]()
and
![]()
we obtain
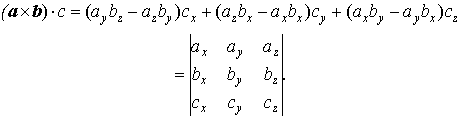
Geometric Interpretation: The absolute
value of the number ![]() is the volume of the parallelepiped
constructed on the vectors a, b
and c as it is shown in the figure below:
is the volume of the parallelepiped
constructed on the vectors a, b
and c as it is shown in the figure below:
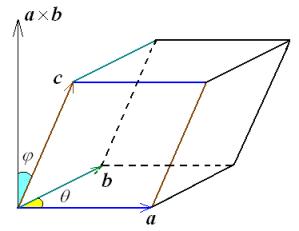
Proof: The volume of a parallelepiped is equal to the product of the area of the base and its height.
By the theorem of scalar product,
![]() ,
,
where the quantity ![]() equals the area of the parallelogram,
and the product
equals the area of the parallelogram,
and the product ![]() equals the height of the parallelepiped.
equals the height of the parallelepiped.
Hence, the theorem.
Corollary: If three vectors are complanar then the scalar triple product is equal to zero.