Determine whether the points , , , and lie on the same plane.

Solution: Join the point A with the other points to obtain the vectors

, , and .

Then find the scalar triple product:

.

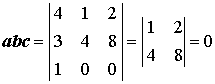Therefore, the vectors lie on a plane, that means the given points lie on the same plane.

Example 2

Find the volume V of a tetrahedron with the vertices at the points , , , and .

Solution: Consider a parallelepiped whose adjacent vertices are at the given points. The volume of the parallelepiped is equal to the absolute value of the triple scalar product of the vectors .

The volume of the tetrahedron is given by the formula

.

Since

, , and ,

we obtain

.

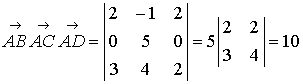Therefore,

.