1) Let i = {1, 0, 0} be the unit vector in the positive direction of the x-axis.

Then any vector can be expressed in the form

.

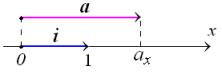
In such a case the vector i is said to be a basis in an one-dimensional space of vectors.

2) Let i = {1, 0, 0} and j = {0, 1, 0} be two unit vectors in the positive directions of the x-axis and y-axis, correspondingly.

Then any vector can be expressed in the form

.

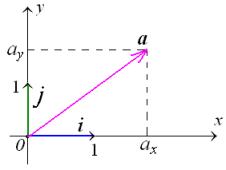
They say that i and j are basis vectors in a two-dimensional space of vectors.

3) Let i = {1, 0, 0}, j = {0, 1, 0}, and k = {0, 0, 1} be three unit vectors in the positive directions of the corresponding coordinate axes.

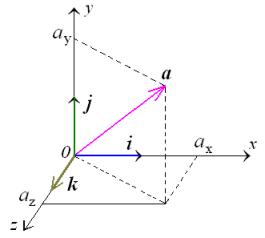
Then any vector can be expressed as the linear combination of the vectors i, j and k:

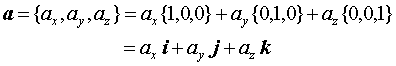
Note that i, j and k are mutually orthogonal (perpendicular) unit vectors. The set of vectors i, j and k is called a rectangular orthogonal basis.

The above formulas describe the decomposition of a vector over basis vectors.