Example 2. The figure below illustrates the general property of symmetry of two mutually inverse functions:
The graphs of a function and its inverse are reflections of one another
off the mirror line y = x.
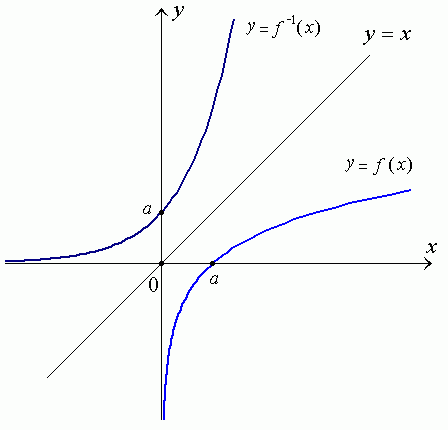
| Inverse Functions |
|
Example 1. Find the inverse functions of y = 7 x – 2 Solution. First, interchange the variables: x = 7 y
– 2
Then solve the equation for y to find the inverse function: y = ( x + 2 ) / 7 Thus,f –
1( x ) = ( x
+ 2 ) / 7.
Check-up.
f ( f
– 1( x
) ) = f ( ( x
+ 2) / 7 ) = 7 ( x + 2) / 7 –
2 = ( x + 2 ) – 2 = x,
|
|
Example 2. The figure below illustrates the general property of symmetry of two mutually inverse functions:
|