Use Gaussian elimination to solve the following homogeneous system of equations.

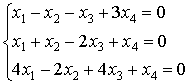
Solution: By elementary transformations, the coefficient matrix can be reduced to the row echelon form

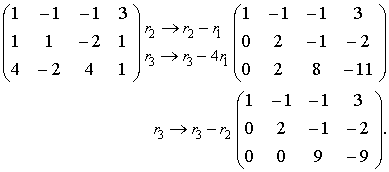
The rank of this matrix equals 3, and so the system with four unknowns has an infinite number of solutions, depending on one free variable. If we choose x4 as the free variable and set x4=c, then the leading unknowns have to be expressed through the parameter c. The above matrix corresponds to the following homogeneous system

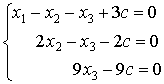
The last equation implies

.

Using the method of back substitution we obtain

,

.

Therefore, the general solution of the given system is given by the following formula:

.

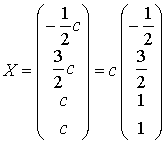To obtain a particular solution x1 we have to assign some value to the parameter c. If c = 4 then

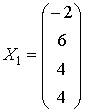
Solution check: Show that the set of values of the unknowns

, , ,

reduces all equations of the given linear system to identities:

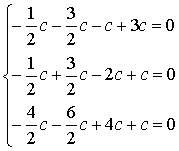
Example 2

Let 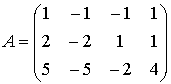. Find the solution of the homogeneous system of linear equations

.

Solution: Transform the coefficient matrix to the row echelon form:

.

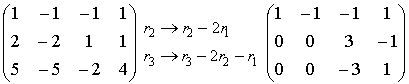
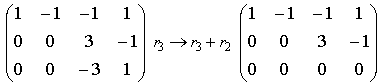Since , we have to consider two unknowns as leading unknowns and to assign parametric values to the other unknowns. Setting x2=c1 and x3=c2 we obtain the following homogeneous linear system:

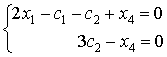
Therefore,

and .

Thus, the given system has the following general solution:

.

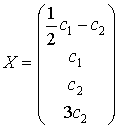In view of the matrix properties, the general solution can be also expressed as the linear combination of particular solutions:

.

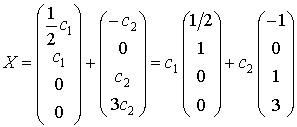The particular solutions

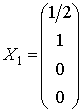and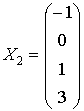

form the fundamental system of solutions.

Thus,

.

Example 3

Let 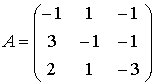. Solve the following homogeneous system of linear equations

.

Explain why there are no solutions, an infinite number of solutions, or exactly one solution.

Solution: Note that any homogeneous system is consistent and has at least the trivial solution.

Transform the coefficient matrix to the triangular or row echelon form.

.

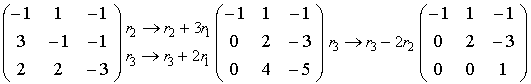The rank of A equals 3. Therefore, there are no free variables and the system

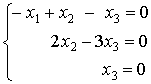
has only the trivial solution:

.