Solve the below system via Gaussian elimination

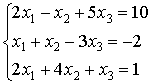
Solution: Reduce the augmented matrix of the system to a triangle form:

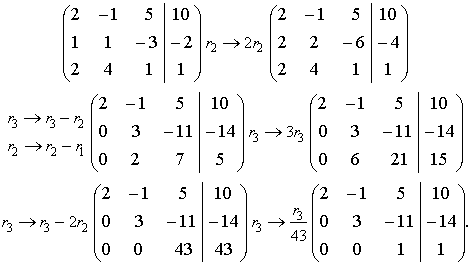
This matrix corresponds to the system

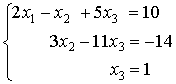
which is equivalent to the initial system.

Now the solution can be easily found:

,

.

Thus we obtain the solution

.

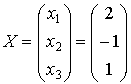It is not difficult to verify that this set of values of the unknowns satisfies all the given equations.

Example 2

Find all solutions of the system of equations via Gaussian elimination

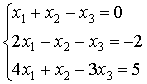
Solution: The system can be represented by the augmented matrix. Applying the linear row operations we obtain

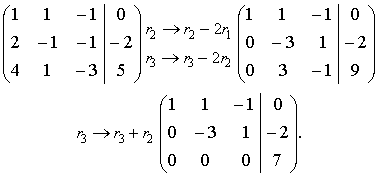
The third row corresponds to the equation

which has no solutions.

Therefore, the given system is inconsistent.

Example 3

Use Gaussian elimination to solve the system of equations

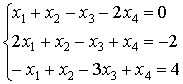
Solution: By elementary transformations the augmented matrix can be reduced to the row echelon form

This matrix has the rank 3 and corresponds to the system

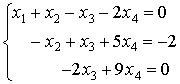
From the last equation we find

.

Then we obtain

,

.

The variable x4 can be considered as an arbitrary parameter c, regardless of the value of which the remaining values of x1, x2 and x3 reduce all equations of the given system to identities.

Thus the system has the following general solution:

.

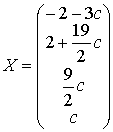Any particular value of c gives a particular solution of the system. Setting, for instance, c = 0 we obtain a particular solution

.

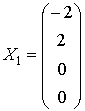If c = 2 then we get a particular solution

.

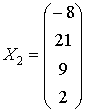Conclusion: The given system has infinitely many solutions.

Solution check: Let us verify that the set of values

, , ,

satisfies the given system of equations:

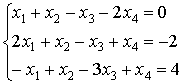
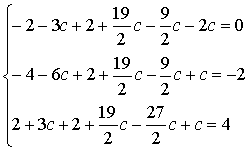
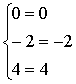
That is true.