Matrices in the reduced row echelon form:

, ,

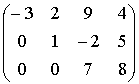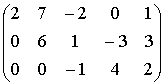
Example 2

Determine the rank of the matrix

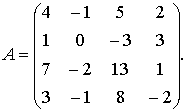
Solution: Subtracting the first and fourth rows from the third one, we find that

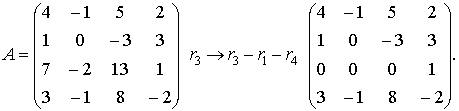
Multiply the third row by suitable numbers and add the results to the other rows:

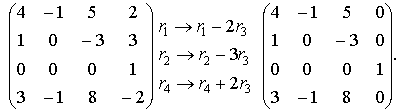
Subtract the first row from the fourth row and then add the second row to the fourth one:

It is clear that there exists a nonzero determinant of a submatrix of the order 3, e.g.,

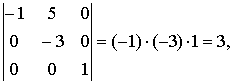
while the determinant of the order 4 is equal to zero.

Hence,

rank A =3.