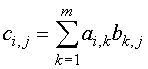| Equality of Matrices |
 |
Two matrices of the same size, 
and 
, are equal if their corresponding
elements are equal, that is,
 for each pair of indexes {i,j} |
| Scalar Multiplication |
|
Any matrix A may be multiplied on the right
or left by a scalar 
. Then the product 
is the matrix 
of the same size as A
and such that
for each pair of indexes {i, j}.
|
To multiply a matrix by a number, multiply every
element by the given number
|
| The Sum of Matrices |
|
The sum of any two 
matrices 
and 
is the 
matrix 
such that
for each pair of indexes {i, j}.
|
To add matrices, add the corresponding elements.
|
| Multiplication of a Row by a Column |
|
Let A be a row matrix having as many elements as a column matrix B. In order to multiply A by B, it is necessary to multiply the corresponding elements of the matrices and to add up the products. Symbolically,
 |
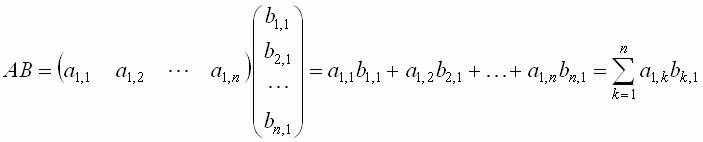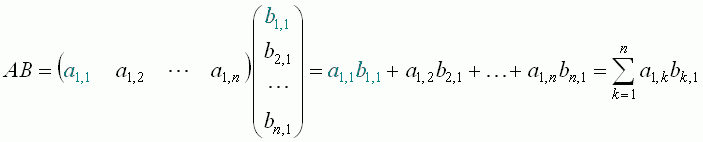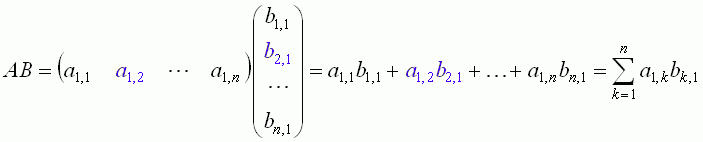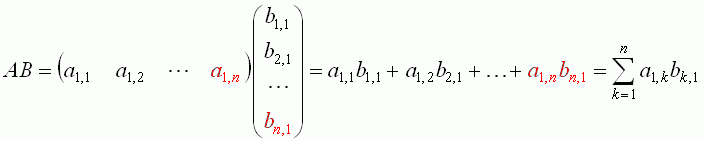Thus, multiplying a row matrix by a column matrix we obtain a number. Later we will show that any number can be considered as an 1x1 matrix.
To multiply a two-row matrix
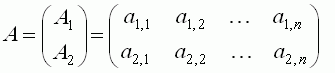
by the column matrix
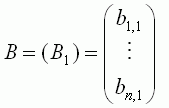
we multiply each row of A by the column of B. In this case, the product AB is the following 2 x 1matrix:
.
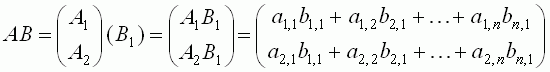Similarly, the multiplication of an m-row matrix by a n-column matrix generate the m x n matrix.
| Matrix Multiplication |
|
Let A be a 
matrix and let B
be a 
matrix. Since A
has l rows and B
has n columns, the product C = AB
is the 
matrix. If we denote the rows of
A by 
and the columns of B
by 
, then
,
,
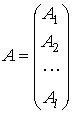and
|
To find the element on the i-th row and the j-th column of the product C = AB, multiply the i-th row of A by the j-th column of B, that is, |
The matrix product AB is defined only if the number of columns of A is equal to the number of rows of B.
Note 1: The symbolic notation 
means the product of two equal square
matrices:
.
Similarly,
, 
.
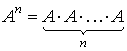Note 2: In the general case, the product of matrices is not commutative:
.
